如图所示,“神舟”飞船升空后,进入近地点为B,远地点为A的椭圆轨道I上飞行。飞行数圈后变轨.在过远地点A的圆轨道Ⅱ上做匀速圆周运动。飞船由椭圆轨道运行变轨到圆形轨道运行后
A周期变短.机械能增加
B周期变短,机械能减小
C周期变长,机械能增加
D.周期变长,机械能减小
欧盟和我国合作的“伽利略”全球定位系统的空间部分由平均分布在三个轨道面上的30颗轨道卫星组成,每个轨道平面上等间距部署10颗卫星,从而实现高精度的导航定位,现假设“伽利略”系统中每颗卫星均绕地心O做匀速圆周运动,一个轨道平面上某时刻10颗卫星所在位置分布如图所示。若卫星均顺时针运行,地球表面处的重力加速度为g,不计卫星间的相互作用力。
则以下判断中正确的是
| A.这些卫星的运行速度均小于7.9km/s |
| B.这些卫星的加速度大小均小于g |
| C.这些卫星处于完全失重状态 |
| D.若已知这些卫星的周期和轨道半径,可求出卫星的质量 |
两颗人造卫星A、B绕地球做圆周运动,周期之比为TA:TB=1:8,则轨道半径之比和运行速度之比分别为:
A.rA:rB ="4:1" , VA:VB ="1:2 " B.rA:rB ="4:1" , VA:VB ="2:1"
C.rA:rB ="1:4" , VA:VB ="1:2 " D.rA:rB ="1:4" , VA:VB ="2:1"
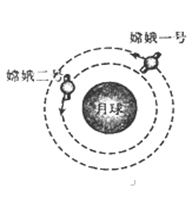
2010年10月1日19时整“嫦娥二号”成功发射。其环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加翔实。若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示。则( )
| A.“嫦娥二号”环月运行的周期比“嫦娥一号”大 |
| B.“嫦娥二号”环月运行的线速度比“嫦娥一号”小 |
| C.“嫦娥二号”环月运行的向心加速度比“嫦娥一号”大 |
| D.“嫦娥二号”环月运行的向心力与“嫦娥一号”相等 |
质量相等的两颗人造地球卫星A和B,分别在不同轨道上绕地球做匀速圆周运动,两卫星的轨道半径分别为rA和rB,且rA>rB,则A和B两卫星比较,下列说法正确的是( )
| A.卫星A受到地球引力较小 | B.卫星A的动能较小 |
| C.卫星B的运动周期较大 | D.卫星A的机械能较小 |
我国将于2011年11月发射“天宫一号”目标飞行器,随后将发射“神舟八号”飞船并与“天宫一号”实现对接。某同学得知上述消息后,画出“天宫一号”和“神舟八号”绕地球做匀速圆周运动的假想图如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道。由此假想图,可以判定( )
| A.“天宫一号”的运行速率小于“神舟八号”的运行速率 |
| B.“天宫一号”的周期小于“神舟八号”的周期 |
| C.“天宫一号”的向心加速度大于“神舟八号”的向心加速度 |
| D.“神舟八号”从图示轨道运动到与“天宫一号”对接过程中机械能守恒 |
2008年9月25日,我国利用“神州七号”飞船将翟志刚、刘伯明、景海鹏三名宇航员送入太空。设宇航员测出自己绕地球做圆周运动的周期为T,离地高度为H,地球半径为R,则根据T、H、R和引力常量G,能计算出的物理量是 ( )
| A.地球的质量 | B.地球的平均密度 |
| C.飞船所需的向心力 | D.飞船线速度的大小 |
“嫦娥二号”探月卫星于2010年10月1日18时59分在西昌卫星中心发射升空,沿地月转移轨道直奔月球,6日在距月球表面100 km的近月点P处,第一次“刹车制动”后被月球捕获,进入椭圆轨道I绕月飞行。这次减速只有一次机会,如果“刹车”力度不够,卫星会飞出月球的引力范围,不被月球捕获,从而不能环绕月球运动。如果刹车力度过大,卫星就可能撞上月球,其后果同样不堪设想。之后卫星在P点又经过两次“刹车制动”,最后在距月球表面100km的圆形轨道Ⅲ上绕月球做匀速圆周运动,其整个过程的运动轨迹如图所示。下列说法中正确的是
| A.实施第一次“刹车”的过程,将使“嫦娥二号”损失的动能转化为势能,转化过程中机械能守恒 |
| B.第一次“刹车制动”如果不能减速到一定程度,月球对它的引力将会做负功 |
| C.因经多次“刹车”,故卫星在轨道Ⅲ上运动的周期比在轨道I上长 |
| D.卫星在轨道Ⅲ上运动到P点时的加速度小于沿轨道I运动到P点时的加速度 |
均匀分布在地球赤道平面上空的三颗同步通信卫星能够实现除地球南北极等少数地区外的“全球通信”。已知地球半径为R,地球表面的重力加速度为g,同步卫星所在轨道处的重力加速度为g′,地球自转周期为T,下面列出的是关于三颗卫星中任意两颗卫星间距离s的表达式,其 中正确的是( )
中正确的是( )
A.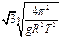 |
B.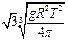 |
C.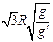 |
D.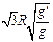 |
我国于2010年1月17日在西昌卫星发射中心成功发射了第三颗北斗导航卫星.该卫星在发射过程中经过四次变轨进入同步轨道.如图为第四次变轨的示意图,卫星先沿椭圆轨道I飞行,后在远地点P处实现变轨,由椭圆轨道I进人同步轨道II则该卫星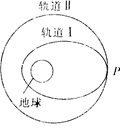
| A.在轨道Ⅱ上的周期比在轨道I上的周期小 |
| B.在轨道Ⅱ上的加速度比在轨道I上任意—点的加速度都大 |
| C.在轨道Ⅱ上的机械能比在轨道I上任意一点的机械能都大 |
| D.在轨道Ⅱ上的速度比在轨道I上任意—点的速度都大 |
三颗卫星都在赤道平面内绕地球做匀速圆周运动,它们的轨道半径分别为r1、r2、r3,且r1>r2>r3,r2为同步卫星的轨道半径,三颗卫星在运动过程受到的向心力大小相等,则
| A.经过相同的时间,卫星1通过的路程最大 | B.三颗卫星中,卫星1的质量最大 |
| C.三颗卫星中,卫星1的加速度最大 | D.卫星3的周期小于24小时 |
人类为探测月球是否存在水分,于2009年10月9日利用一支火箭和一颗卫星连续撞击月球。据天文学家测量,月球的半径约为1800km,月球表面的重力加速度约为地球表面重力加速度的1/6,月球表面在阳光照射下的温度可达127°C,而此时水蒸气分子的平均速率达2 km/s,下列说法正确的是
| A.卫星撞月前应先在原绕月轨道上加速 |
| B.卫星撞月前应先在原绕月轨道上减速 |
| C.由于月球的第一宇宙速度大于2 km/s,所以月球表面可能有水 |
| D.由于月球的第一宇宙速度小于2 km/s,所以月球表面在阳光照射下不可能有水 |
已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
⑴推导第一宇宙速度 的表达式;
的表达式;
⑵若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求卫星的运行周期T。
两颗卫星在同一轨道平面绕地球作匀速圆周运动,地球半径为R,a卫星离地面的高度为R,b卫星离地面的高度为3R,则
(1)a、b两卫星运行的线速度大小之比Va∶Vb是多少?
(2)a、b两卫星的周期之比Ta∶Tb是多少?
(3)a、b两卫星所在轨道处的重力加速度大小之比ga∶gb是多少?
2010年10月1日,“嫦娥二号”探月卫星成功发射.若“嫦娥二号”沿圆形轨道绕月球飞行的半径为R,国际空间站沿圆形轨道绕地球做匀速圆周运动的半径为4R,地球质量是月球质量的81倍,根据以上信息可以确定
| A.“嫦娥二号”的加速度比国际空间站的加速度大 |
| B.“嫦娥二号”的速度比国际空间站的速度大 |
| C.“嫦娥二号”绕月球的运行周期比国际空间站绕地球的运行周期长 |
| D.“嫦娥二号”的角速度比国际空间站的角速度大 |