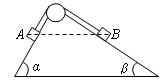
如图所示,A、B两物体用一根跨过定滑轮的细绳相连,置于固定斜面体的两个斜面上的相同高度,处于静止状态,两斜面的倾角分别为37°和53°,若不计摩擦,剪断细绳后,下列说法中正确的是(以地面为参考面)( )
| A.两物体着地时的速度相同 |
| B.两物体着地时的速率相同 |
| C.两物体着地时的机械能一定不同 |
| D.两物体着地时的动能一定相同 |
出行是人们工作生活必不可少的环节,出行的工具五花八门,使用的能源也各不相同。某品牌电动自行车的铭牌如下:
| 车型:20吋(车轮直径:508 mm) |
电池规格:36 V 12 Ah(蓄电池) |
| 整车质量:40 kg |
额定转速:210 r/min(转/分) |
| 外形尺寸:L 1800 mm×W 650 mm×H 1100 mm |
充电时间:2~8 h |
| 电机:后轮驱动、直流永磁式电机 |
额定工作电压/电流:36 V/5 A |
根据此铭牌中的有关数据,可知该车的额定时速约为( )
| A.15 km/h | B.18 km/h | C.20 km/h | D.25 km/h |
下列说法正确的是
| A.由能量守恒定律可知,能量不能无中生有 |
| B.风能、水能是太阳能的间接形式 |
| C.人类通过不断努力,永动机是可以制造出来的 |
| D.能量耗散反映了自然界能量转化的方向性 |
关于弹性势能,下列说法正确的是 ( )
| A.弹性势能与物体的形变量有关 | B.弹性势能与物体的形变量无关 |
| C.物体运动的速度越大,弹性势能越大 | D.物体运动的速度越大,弹性势能越小 |
以初速度v0竖直向上抛出一个质量为m的小球,小球运动过程中所受阻力f的大小不变,上升的最大高度为h,则抛出过程中,人手对小球做的功为(设急速抛出):( )
A.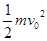 |
B.mgh | C.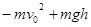 |
D.mgh+fh |
如图所示,一个物体以速度v0冲向竖直墙壁,墙壁和物体间的弹簧被物体压缩,在此过程中以下说法正确的是( )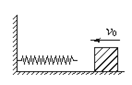
| A.物体对弹簧做的功与弹簧的压缩量成正比 |
| B.物体向墙壁运动相同的位移,弹力做的功不相等 |
| C.弹力做正功,弹簧的弹性势能减小 |
| D.弹簧的弹力做负功,弹性势能增加 |
在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面几个实例中应用到这一思想方法的是( )
A.由加速度的定义 ,当 ,当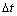 非常小, 非常小,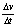 就可以表示物体在t时刻的瞬时加速度 就可以表示物体在t时刻的瞬时加速度 |
| B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 |
| C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 |
| D.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点 |
质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力的作用。设某一时刻小球通过轨道的最低点,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点,则在此过程中小球克服空气阻力所做的功为:( )
A.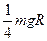 |
B.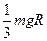 |
C.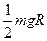 |
D.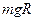 |
两块材料相同的物块A、B,放在水平粗糙地面上,在力F作用下一同前进,如图示,其质量之比为mA:mB="2:1" 在运动过程中,力F一共对物体做功300J,则A对B的弹力对B所做的功一定( )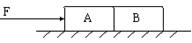
A.100J B.150J
C.300J D.条件不足,无法判断
如图所示,质量为m的物块,始终固定在倾角为α的斜面上,下面说法中正确的是( )
①若斜面向左匀速移动距离s,斜面对物块没有做功
②若斜面向上匀速移动距离s,斜面对物块做功mgs
③若斜面向左以加速度a移动距离s,斜面对物块做功mas
④若斜面向下以加速度a移动距离s,斜面对物块做功m(g+a)s
| A.①②③ | B.②④ | C.②③④ | D.①③④ |
用力将重物竖直提起,先是从静止开始匀加速上升,紧接着匀速上升.如果前后两过程的运动时间相同,不计空气阻力,则( )
| A.加速过程中重力的功一定比匀速过程中拉力的功大 |
| B.匀速过程中重力的功比加速过程中重力的功大 |
| C.两过程中拉力的功一样大 |
| D.以上情况都不正确 |
一物体在竖直弹簧的上方h米处下落,然后又被弹簧弹回,则物体动能最大时是( )
| A.物体刚接触弹簧时 | B.物体将弹簧压缩至最短时 |
| C.物体重力与弹力相等时 | D.弹簧等于原长时 |
关于对动能的理解,下列说法正确的是( )
| A.动能是机械能的一种表现形式,凡是运动的物体都具有动能 |
| B.动能总为正值 |
| C.一定质量的物体,动能变化时,速度一定变化;但速度变化时,动能不一定变化 |
| D.动能不变的物体,一定处于平衡状态 |