关于弹性势能,下列说法正确的是 ( )
| A.弹性势能与物体的形变量有关 | B.弹性势能与物体的形变量无关 |
| C.物体运动的速度越大,弹性势能越大 | D.物体运动的速度越大,弹性势能越小 |
物体从高出地面H处,由静止自由下落,如图所示,不考虑空气阻力,落至地面进入沙坑深h处停止,求物体在沙坑中受到的平均阻力是其重力的多少倍?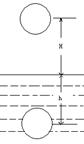
质量m="1" t的小汽车,以额定功率行驶在平直公路上的最大速度是vm1="12" m/s,以额定功率开上每前进20 m升高1 m的山坡时最大速度是vm2="8" m/s.如果这两种情况中车所受到的摩擦力相等,求:
(1)汽车发动机的额定功率.
(2)摩擦阻力.
(3)车沿原山坡以额定功率下行时的最大速度vm3.(g取10 m/s2)
如图所示,质量是20kg的小车,在一个与斜面平行的200N的拉力作用下,由静止开始前进了3m,斜面的倾角为300,小车与斜面间的摩擦力忽略不计.求这一过程物体的重力势能增加了多少?物体的动能增加了多少? 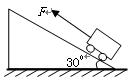
如图所示,劲度系数为k的轻质弹簧一端固定,另一端与物块拴接,物块保持静止放在光滑水平面上。现用外力缓慢拉动物块,若外力所做的功为W,则物块移动的距离为 。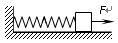
以初速度v0竖直向上抛出一个质量为m的小球,小球运动过程中所受阻力f的大小不变,上升的最大高度为h,则抛出过程中,人手对小球做的功为(设急速抛出):( )
A.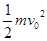 |
B.mgh | C.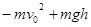 |
D.mgh+fh |
如图所示,一个物体以速度v0冲向竖直墙壁,墙壁和物体间的弹簧被物体压缩,在此过程中以下说法正确的是( )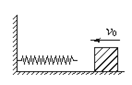
| A.物体对弹簧做的功与弹簧的压缩量成正比 |
| B.物体向墙壁运动相同的位移,弹力做的功不相等 |
| C.弹力做正功,弹簧的弹性势能减小 |
| D.弹簧的弹力做负功,弹性势能增加 |
在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面几个实例中应用到这一思想方法的是( )
A.由加速度的定义 ,当 ,当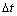 非常小, 非常小,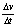 就可以表示物体在t时刻的瞬时加速度 就可以表示物体在t时刻的瞬时加速度 |
| B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 |
| C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 |
| D.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点 |
质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力的作用。设某一时刻小球通过轨道的最低点,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点,则在此过程中小球克服空气阻力所做的功为:( )
A.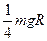 |
B.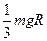 |
C.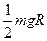 |
D.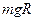 |
两块材料相同的物块A、B,放在水平粗糙地面上,在力F作用下一同前进,如图示,其质量之比为mA:mB="2:1" 在运动过程中,力F一共对物体做功300J,则A对B的弹力对B所做的功一定( )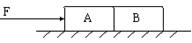
A.100J B.150J
C.300J D.条件不足,无法判断
如图所示,质量为m的物块,始终固定在倾角为α的斜面上,下面说法中正确的是( )
①若斜面向左匀速移动距离s,斜面对物块没有做功
②若斜面向上匀速移动距离s,斜面对物块做功mgs
③若斜面向左以加速度a移动距离s,斜面对物块做功mas
④若斜面向下以加速度a移动距离s,斜面对物块做功m(g+a)s
| A.①②③ | B.②④ | C.②③④ | D.①③④ |
用力将重物竖直提起,先是从静止开始匀加速上升,紧接着匀速上升.如果前后两过程的运动时间相同,不计空气阻力,则( )
| A.加速过程中重力的功一定比匀速过程中拉力的功大 |
| B.匀速过程中重力的功比加速过程中重力的功大 |
| C.两过程中拉力的功一样大 |
| D.以上情况都不正确 |
一物体在竖直弹簧的上方h米处下落,然后又被弹簧弹回,则物体动能最大时是( )
| A.物体刚接触弹簧时 | B.物体将弹簧压缩至最短时 |
| C.物体重力与弹力相等时 | D.弹簧等于原长时 |