高中物理力的合成选择题

如图所示，光滑半球形容器固定在水平面上，O为球心，一质量为m的小滑块，在水平力F的作用静止与P点，设滑块所受支持力为，OP与水平方向的夹角为，下列关系正确的是

A．

B．

C．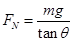

D．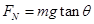

关于轮船渡河，正确的说法是（      ）

A．水流的速度越大，渡河的时间越长

B．欲使轮船垂直驶达对岸，船头的指向应垂直河岸

C．欲使渡河时间越短，船头的指向应垂直河岸

D．轮船相对水的速度越大，渡河的时间一定越短

将力F分解成F₁和F₂，若已知F₁的大小和F₂与F的夹角θ（θ为锐角)，则下列判断不正确的是（ ）

A．当F1＞Fsinθ时，有两解

B．当F1=Fsinθ时，一解

C．当Fsinθ＜F1＜F时，有两解

D．当F1＜Fsinθ时，无解

如图所示是骨折病人的牵引装置示意图，绳的一端固定，绕过定滑轮和动滑轮后挂着一个重物，与动滑轮相连的帆布带拉着病人的脚，整个装置在同一竖直平面内．为了使脚所受的拉力减小，可采取的方法是（ ）

A．只增加绳的长度	B．只减小重物的质量
C．只将病人的脚向左移动	D．只将两定滑轮的间距增大

如图所示，重力为G的质点M，与三根劲度系数相同的螺旋弹簧A、B、c相连，C处于竖直方向，静止时，相邻弹簧间的夹角均为120°，已知弹簧A和B对质点的作用力的大小均为2G，则弹簧C对质点的作用力的大小可能为（ ）

A．2G    B．G    C．O    D．3G

如图所示，开口向下的“┍┑”形框架，两侧竖直杆光滑固定，上面水平横杆中点固定一定滑轮，两侧杆上套着的两滑块用轻绳绕过定滑轮相连，并处于静止状态，此时连接滑块A的绳与水平方向夹角为θ，连接滑块B的绳与水平方向的夹角为2θ，则A、B两滑块的质量之比为（    ）

A．2sinθ：1        B．2cosθ：1         C．1：2cosθ      D．1：2sinθ

作用在同一物体上的两个力，F₁=5N，F₂=10N，用一个力等效替代这两个力，则这个力不可能是（ ）

A．4N

B．6N

C．15N

D．17N

如图所示，保持两个共点力大小不变，使两者的夹角从60°逐渐增大到120°，则在此过程中，其合力大小

A．逐渐增大

B．逐渐减小

C．先增大后减小

D．先减小后增大

两个共点力的大小分别是5N和8N，这两个力的合力大小不可能

A．5N

B．8N

C．12N

D．14N

某同学为探究求合力的方法，做了如图所示的实验．ABCD为竖直平板，E、F两处固定了摩擦不计的轻质滑轮，滑轮的轴保持水平，所用绳子的质量可不计．第一次实验中，当装置平衡时，绳子的结点在O处，拉力的方向和钩码的位置如图所示．第二次实验时，仅把右侧滑轮的位置移动到图中的G点，待稳定后，∠EOF将      （填“变大”、“变小”或“不变”），绳子结点O的位置将

A．竖直向下移动

B．水平向右移动

C．沿EO方向移动

D．沿FO方向移动．

如图所示，质量为m的小球，与三根相同的轻弹簧相连．静止时，弹簧c沿竖直方向，相邻两弹簧轴线间的夹角均为120°.已知弹簧a、b对质点的作用力大小均为F，则弹簧c对小球的作用力大小

A．可能为F ，也可能为F＋mg

B．可能为F ，一定不可能为F＋mg

C．可能为F－mg，一定不可能为mg－F

D．可能为mg－F，也可能为F－mg

现在城市的滑板运动非常流行，在水平地面上一名滑板运动员双脚站在滑板上以一定速度向前滑行，在横杆前起跳并越过杆，从而使人与滑板分别从杆的上下通过，如图所示．假设人和滑板运动过程中受到的各种阻力忽略不计，运动员能顺利完成该动作，最终仍落在滑板原来的位置上，要使这个表演成功，运动员除了跳起的高度足够外，在起跳时双脚对滑板作用力的合力方向应该

A．竖直向上	B．向下适当偏后
C．竖直向下	D．向上适当偏前

如图所示，细绳下悬挂一小球D，小球与光滑的静止斜面接触，且细绳处于竖直状态，则下列说法中正确的是（   ）

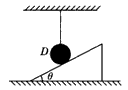
A．斜面对D的支持力垂直于斜面向上

B．D对斜面的压力竖直向下

C．D与斜面间无相互作用力

D．因D的质量未知，所以无法判定斜面对D支持力的大小和方向

如图所示，轻弹簧的两端各受20N拉力F的作用，弹簧伸长了10cm（在弹性限度内）．那么下列说法中正确的是（ ）

A．弹簧所受的合力为零

B．弹簧所受的合力为20N

C．该弹簧的劲度系数k为200N/m

D．根据公式k=，弹簧的劲度系数k会随弹簧弹力F的增大而增大

共点的三个力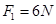、、，则、、三力的合力的范围是

A．	B．
C．	D．