在高中物理力学实验中,下列说法中正确的是
| A.利用打点计时器在“研究匀变速直线运动规律”的实验中,可以根据纸带上的点迹计算物体的平均速度 |
| B.在“验证力的平行四边形定则”实验中,要使力的作用效果相同,只需橡皮条具有相同的伸长量 |
| C.在“验证牛顿第二定律”的实验中,需要先平衡摩擦力 |
| D.在“验证机械能守恒定律”的实验中,应该先释放重物后接通电源 |
如图所示,A、B、C三球质量均为m,轻质弹簧一端固定在斜面顶端、另一端与A球相连,A、B间固定一个轻杆,B、C间由一轻质细线连接。倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,下列说法正确的是( )

A.A球的受力情况未变,加速度为零
B.C球的加速度沿斜面向下,大小为g
C.A、B之间杆的拉力大小为
D.A、B两个小球的加速度均沿斜面向上,大小均为
如图所示,吊床用绳子拴在两棵树上等高位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳中的拉力为F1、吊床对该人的作用力为F2,则( )
| A.坐着比躺着时F1大 | B.躺着比坐着时F1大 |
| C.坐着比躺着时F2大 | D.躺着比坐着时F2大 |
如图所示,光滑半球形容器固定在水平面上,O为球心.一质量为m的小滑块,在水平力F的作用下静止于P点.设滑块所受支持力为FN,OP与水平方向的夹角为θ.下列关系正确的是 ( )

A. |
B.F=mg tan θ | C.FN= |
D.FN=mg tan θ |
如图所示,在倾角为30°的足够长的斜面上有一质量为m的物体,它受到沿斜面方向的力F的作用。力F可按图(a)、(b)、(c)、(d)所示的四种方式随时间变化(图中纵坐标是F与mg的比值,力沿斜面向上为正)。已知此物体在 时速度为零,若用
时速度为零,若用 、
、 、
、 、
、 分别表示上述四种受力情况下物体在
分别表示上述四种受力情况下物体在 末的速率,则这四个速率中最大的是( )
末的速率,则这四个速率中最大的是( )

A. |
B. |
C. |
D. |
(6分)在医院里常用如下图所示装置对小腿受伤的病人进行牵引治疗.不计滑轮组的摩擦和绳子的质量,绳子下端所挂重物的质量是5 kg.问:病人的腿所受水平方向的牵引力是多大?(g=10m/s2)
在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去的速度为v1,摩托艇在静水中的速度为v2,如图所示.战士救人地点A离岸边最近处的距离为d.如战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为( )
A. |
B.0 | C. |
D. |
如图所示,某人由A点划船渡河,假设河的宽度d=30m,船在静水中的速度V1=5m/s,水流的速度V2=3m/s,求:
(1)若船头指向垂直河岸,则船过河的时间为多少?到达的地点与B点的距离为多少?
(2)若改变船头的指向,当船以最短位移过河时,所需要的时间为多少?
关于运动的合成和分解,下述说法中正确的是 ( )
| A.合运动的速度大小等于分运动的速度大小之和 |
| B.物体的两个分运动若是直线运动,则它的合运动一定是直线运动 |
| C.合运动和分运动具有同时性 |
| D.曲线运动的物体受到的合外力一定是变力 |
如图所示,物体A和B的质量均为m,且分别与轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦).当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,以下说法正确的是 ( )
| A.物体A也做匀速直线运动 |
| B.绳子拉力始终大于物体A所受的重力 |
| C.绳子对A物体的拉力逐渐增大 |
| D.绳子对A物体的拉力逐渐减小 |
如图所示,是一名登山运动员的攀登陡峭雪壁的情形,如果认为峭壁的平面是竖直的平面,冰面是光滑的,腿与峭壁面是垂直的,轻绳与壁面的夹角为30°,运动员重为80kg。则细绳给人的张力大小T。
A.T= |
B.T=800N | C.T= |
D.T=1600N |
(1)“验证力的平行四边形定则”实验中,部分实验步骤如下,请完成有关内容:
A.将一根橡皮筋的一端固定在贴有白纸的竖直平整木板上,另一端拴上两根细线
B.其中一根细线挂上5个质量相等的钩码,使橡皮筋拉伸,如图甲所示,记录: 、 、 ;
C.将步骤B中的钩码取下,分别在两根细线上挂上4个和3个质量相等的钩码,用两光滑硬棒B、C使两细线互成角度,如图乙所示,小心调整B、C的位置,使 ,记录 ;
(2)如果“力的平行四边形定则”得到验证,那么图乙中cosα∶cosβ= ;
⑶用平木板、细绳套、橡皮筋、测力计等做“验证力的平行四边形定则”的实验,为了使实验能够顺利进行,且尽量减小误差,你认为下列说法或做法能够达到上述目的的是 。
A.用测力计拉细绳套时,拉力应沿弹簧的轴线,且与水平木板平行
B.两细绳套必须等长
C.同一次实验两次拉细绳套须使结点到达同一位置
D.用测力计拉两个细绳套时,两拉力夹角越大越好
由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心
在三角形所在的平面内做相同角速度的圆周运动(图示为
、
、
三颗星体质量不相同时的一般情况)。若A星体质量为
,
、
两星体的质量均为
,三角形边长为
。求:
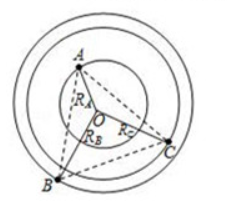
(1) 星体所受合力大小 ;
(2)
星体所受合力大小
;
(3)
星体的轨道半径
;
(4)三星体做圆周运动的周期
。