一物体从某行星表面竖直向上抛出.从抛出瞬间开始计时,得到物体相对于抛出点的位移 与所用时间
与所用时间 的关系如图所示,以下说法中正确的是( )
的关系如图所示,以下说法中正确的是( )
| A.物体上升的最大高度为16m |
| B.该行星表面的重力加速度大小为4m/s2 |
| C.8s末物体上升到最高点 |
| D.物体抛出时的初速度大小为4m/s |
在以速度v上升的电梯内竖直向上抛出小球,电梯内的人看见小球经t秒后到达最高点,则有
| A.地面上的人看见小球抛出时的初速度为v0=gt |
| B.电梯中的人看见小球抛出的初速度为v0=gt |
C.地面上的人看见小球上升的最大高度为h= gt2 gt2 |
| D.地面上的人看见小球上升的时间也为t |
一个从地面竖直上抛的物体,它两次经过一个较低的点a的时间间隔是Ta,两次经过一个较高点b的时间间隔是Tb,则A.b之间的距离为( )
不考虑空气阻力,竖直上抛运动的物体到达最高点时
| A.速度为零,加速度向上 |
| B.速度为零,加速度向下 |
| C.具有向上的速度和加速度 |
| D.具有向下的速度和加速度 |
从同一高度同时以20m/s的速度抛出两小球,一球竖直上抛,另一球竖直下抛。不计空气阻力,取重力加速度为10m/s2。则它们落地的时间差为
| A.3s | B.4s | C.5s | D.6s |
升降机以加速度a竖直向上做匀加速运动,当速度为v时,有一螺帽从升降机的顶部脱落,这时螺帽相对地的加速度和速度大小分别为( )
| A.g-a,v | B.g+a,v | C.a,0 | D.g,v |
一位同学为了测算卫星在月球表面附近做匀速圆周运动的环绕速度,提出了如下实验方案:在月球表面以初速度v0竖直上抛一个物体,测出物体上升的最大高度h,已知月球的半径为R,便可测算出绕月卫星的环绕速度。按此方案,绕月卫星的环绕速度为 ( )
A.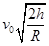 |
B.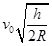 |
C. |
D. |
在地质、地震、勘探、气象和地球物理等领域的研究中,需要精确的重力加速度g值,g值可由实验精确测定,近年来测g值的一种方法叫“对称自由下落法”,它是将测g归于测长度和时间,以稳定的氦氛激光的波长为长度标准,用光学干涉的方法测距离,以铷原子钟或其他手段测时间,能将g值测得很准,具体做法是:将真空长直管沿竖直方向放置,自其中O点竖直向上抛出小球,小球又落至原处O点的时间为 ,在小球运动过程中经过比O点高H的P点,小球离开P点后又回到P点所用的时间为
,在小球运动过程中经过比O点高H的P点,小球离开P点后又回到P点所用的时间为 ,测得
,测得 、
、 和H,可求得g等于( )
和H,可求得g等于( )
A. |
B. |
C. |
D. |
将一小球以一定的初速度竖直向上抛出,空气阻力不计。下面四个速度图象中表示小球运动的v-t图象是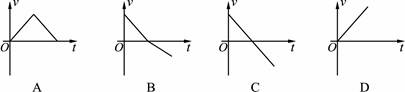
某人在静止的湖面上竖直上抛一小铁球,小铁球上升到最高点后自由下落,穿过湖水并陷入湖底的淤泥中某一深度处.若不计空气阻力,取竖直向上为正方向,则最能反映小铁球运动过程的速度与时间关系的图象是 ( )
如果不计空气阻力,要使一颗礼花弹上升至320 m高处,在地面发射时,竖直向上的初速度至少为(g="10" m/s2) ( )
| A.40 m/s | B.60 m/s |
| C.80 m/s | D.100 m/s |
竖直向上抛出一只小球,3s落回抛出点,则小球在第2s内的位移(不计空气阻力)是( )
| A.10m | B.0m |
| C.-5m | D.-0.25m |
一个从地面上竖直上抛的物体,它两次经过一个较低点A的时间间隔为5s,两次经过一个较高点B时间间隔为3.0s,则AB之间的距离是(g取10m/s2)( )
| A.80m | B.40m | C.20m | D.初速度未知,无法确定 |
如图所示是一个网球沿竖直方向运动时的频闪照片,由照片可知:( )
| A.网球正在上升 | B.网球正在下降 |
| C.网球的加速度向上 | D.网球的加速度向下 |