如图所示,放在水平面上质量为m的物体受一个斜上的拉力F,这个力与水平方向成θ角,在此力作用下,物体水平向右匀速滑动,求:
(1)物体与水平面间的动摩擦因数μ.
(2)如果把此力F撤去,此时物体做什么运动?摩擦力多大?
(3)如果在本题中已知动摩擦因数μ,现只给物体施加一个与水平方向成θ角的斜向下的推力F′,物体仍能保持匀速运动,求F′多大?
如图所示,重为100N的物体受推力F作用贴于墙面静止,F与墙的夹角θ=60°,墙对物体的最大静摩擦力为40N,要使物体保持静止,求推力F的大小范围.
下列说法正确的是( )
| A.弹力的方向不一定与接触面垂直 |
| B.两物体间的滑动摩擦力总是与物体运动方向相反 |
| C.摩擦力的大小与弹力成正比 |
| D.两分力大小一定,夹角越小,合力越大 |
如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l,水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态.可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回.已知R=0.4m,l=2.5m,v0=6m/s,物块质量m=1kg,与PQ段间的动摩擦因数μ=0.4,轨道其它部分摩擦不计.取g=10m/s2.求: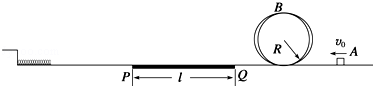
(1)物块经过圆轨道最高点B时对轨道的压力;
(2)物块从Q运动到P的时间及弹簧获得的最大弹性势能;
(3)物块仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动.
如图所示,竖直放置的两块足够长的平行金属板,相距0.08m,两板间的电压是2400V,在两板间的电场中用丝线悬挂着质量是5×10﹣3kg的带电小球,平衡后,丝线跟竖直方向成30°角,若将丝线剪断,则在剪断丝线后,(g取10m/s2)
(1)说明小球在电场中做什么运动;
(2)求小球的带电量;
(3)设小球原来到负极板的距离为0.06m,则经过多少时间小球碰到金属板?
重力为G的物体A受到与竖直方向成α的外力F,如图所示.
(1)若物体A在外力F作用下匀速向上运动,求接触面的动摩擦因数是多少?
(2)若物体A静止在竖直墙面上,求墙对物体A的静摩擦力是多少?
一个重30N的物体置于斜面上,如图,斜面的倾斜角为30°,挡板竖直,不计一切摩擦.(取g=10m/s2)
(1)画出小球受力分析示意图.
(2)求出斜面和挡板对小球的作用力.
如图所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为L,左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场,磁场宽度为s.一质量为m、电阻为r的金属棒MN置于导轨上,与导轨垂直且接触良好,受到F=0.5v+0.4(N)(v为金属棒速度)的水平外力作用,从磁场的左边界由静止开始运动,测得电阻两端电压随时间均匀增大.(已知:L=1 m,m=1 kg,R=0.3 Ω,r=0.2 Ω,s=1 m)
(1)分析并说明该金属棒在磁场中做何种运动;
(2)求磁感应强度B的大小;
(3)若撤去外力后棒的速度v随位移x的变化规律满足v=v0- x,且棒在运动到ef处时恰好静止,则外力F作用的时间为多少?
x,且棒在运动到ef处时恰好静止,则外力F作用的时间为多少?
(4)若在棒未出磁场区域时撤出外力,画出棒在整个运动过程中速度随位移变化所对应的各种可能的图线.
如图所示,在竖直平面内有宽度为L足够长的金属导轨,导轨间有垂直纸面向里的匀强磁场,磁感应强度大小为B0,导轨上有一导体棒在外力作用下以速度v0向左匀速运动;P、Q为竖直平面内两平行金属板,分别用导线和M、N相连,P、Q板长为d,间距也为d, P、Q板间虚线右侧为垂直纸面向里的匀强磁场,磁感应强度大小为B。现有一电量为q的带正电小球,从P、Q左边界的中点水平射入,进入磁场后做匀速圆周运动,重力加速度取g。求:
(1)带电小球的质量m;
(2)能够打在P板上的带电小球在磁场中运动的最短时间;
(3)能够打在P板上的带电小球速度v的取值范围。
如图所示,质量为mA =" 10" kg的A物块下端连接着固定在直立于地面的轻质弹簧,上端连接着跨过定滑轮的轻质细绳,绳的另一端连接着静置于地面、质量为mB =" 20" kg的物块B。此时,与A相连的轻绳处于竖直方向,与B相连的轻绳与水平地面成37°角,并且弹簧的形变量为20 cm,若弹簧劲度系数为k =" 200" N/m,取重力加速度为g =" 10" m/s2,sin 37° = 0.6,cos 37° = 0.8,不计滑轮与轻绳间的摩擦。关于物块B的受力情况,下列分析正确的有: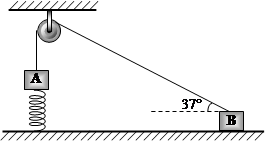
A.轻绳对物块B的拉力一定为60 N
B.地面对物块B的支持力可能为36 N
C.地面对物块B的摩擦力可能为112 N
D.轻绳对物块B的拉力与地面对物块B的摩擦力的合力一定竖直向上
如图所示x轴上各点的电场强度如图所示,场强方向与x轴平行,规定沿x轴正方向为正。一负点电荷从坐标原点O以一定的初速度沿x轴正方向运动,点电荷到达x2位置速度第一次为零,在x3位置第二次速度为零,不计粒子的重力.下列说法正确的是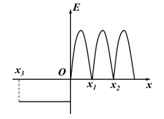
| A.点电荷从O点运动到x2,再运动到x3的过程中,速度先均匀减小再均匀增大,然后减小再增大 |
| B.点电荷从O点运动到x2,再运动到x3的过程中,加速度先减小再增大,然后保持不变 |
C.O点与x2和O点与x3电势差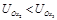 |
| D.点电荷在x2、x3位置的电势能最大 |
小明利用如图甲所示的电路测定旧电池组的电动势与内电阻。
⑴用笔画线代替导线将图乙中的实物连线补充完整;
⑵由图丙可知:该电池组的电动势E= V,内阻r=  (保留两位有效数字);
(保留两位有效数字);


⑶小明又利用上述实验方案测定了同规格新电池组的电动势与内电阻。通过实验发现旧电池组与新电池组相比,电动势几乎没有变化,但它们的输出功率P随外电阻R变化的关系图线有较大差异,如图丁所示。可知图线 (选填“A”或“B”)对应的是新电池组,试说出判断的理由: 。
如图所示,电路中电源电动势为 ,内阻不计,水平放置的平行金属板
,内阻不计,水平放置的平行金属板 、
、 间的距离为
间的距离为 ,金属板长为
,金属板长为 。在两金属板左端正中间位置
。在两金属板左端正中间位置 ,有一个小液滴以某一初速度水平向右射入两板间,已知小液滴的质量为
,有一个小液滴以某一初速度水平向右射入两板间,已知小液滴的质量为 ,带负电,电荷量为
,带负电,电荷量为 。要使液滴从
。要使液滴从 板右侧边缘射出电场,重力加速度用
板右侧边缘射出电场,重力加速度用 表示。求:
表示。求:
(1)两金属板间的电压 ;
;
(2)液滴在电场中运动的加速度;
(3)液滴进入电场时的初速度 。
。
升降机地面上固定着一个倾角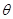 =37º的光滑斜面,用一条平行于斜面的细绳拴住一个质量m=2kg的小球,如图所示,当升降机以加速度a=2m/s2做竖直向上匀加速直线运动时,重力加速度g取10m/s2,
=37º的光滑斜面,用一条平行于斜面的细绳拴住一个质量m=2kg的小球,如图所示,当升降机以加速度a=2m/s2做竖直向上匀加速直线运动时,重力加速度g取10m/s2, ,求:
,求:
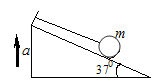
(1)绳子对球的拉力T?
(2)小球对斜面的压力N?
质谱仪是用来测定带电粒子质量和分析同位素的重要工具,如图所示,电容器两极板相距为d,两板间电压为U,极板间匀强磁场的磁感应强度为B1,方向垂直纸面向外。一束电荷电量相同、质量不同的带正电的粒子,沿电容器的中线平行于极板射入电容器,沿直线匀速穿过电容器后进入另一磁感应强度为B2的匀强磁场,磁场方向垂直纸面向外。结果分别打在感光片上的a、b两点,设a、b两点之间距离为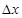 ,粒子所带电荷量为q,且不计重力,求:
,粒子所带电荷量为q,且不计重力,求:
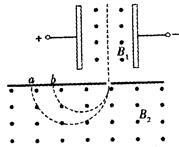
(1)粒子在磁场B1 中直线运动时速度v的大小?
(2)打在a、b两点的粒子的质量之差 ?
?
(3)试比较这两种带电粒子在磁场B2中运动时间的大小关系,并说明理由?