如图所示,光滑斜面上放一轻质弹簧,弹簧下端固定,小球从静止开始沿斜面下滑,从它接触弹簧到弹簧被压缩至最短的过程中,小球的加速度和速度的变化情况是( )
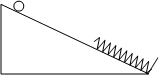
| A.加速度一直变大,速度一直变小 |
| B.加速度一直变小,速度一直变大 |
| C.加速度先变小后变大,速度先变大后变小 |
| D.加速度先变大后变小,速度先变小后变大 |
如图甲所示,为测定物体冲上粗糙斜面能达到的最大位移x与斜面倾角θ的关系,将某一物体每次以不变的初速率沿足够长的斜面向上推出,调节斜面与水平方向的夹角θ,实验测得x与斜面倾角θ的关系如图乙所示,g取10m/s2,根据图象可求出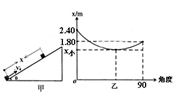
| A.物体的初速率v0=3m/s |
| B.物体与斜面间的动摩擦因数μ=0.75 |
| C.取不同的倾角θ,物体在斜面上能达到的位移x的最小值x小=1.44m |
| D.当某次θ=300时,物体达到最大位移后将沿斜面下滑 |
如图所示,倾角为θ的光滑斜面足够长,一物质量为m小物体,在沿斜面向上的恒力F作用下,由静止从斜面底端沿斜面向上做匀加速直线运动,经过时间t,力F做功为60J,此后撤去力F,物体又经过相同的时间t回到斜面底端,若以地面为零势能参考面,则下列说法正确的是( )
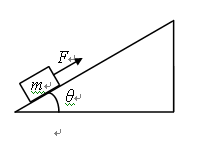
| A.物体回到斜面底端的动能为60J |
| B.恒力F=2mgsinθ |
| C.撤出力F时,物体的重力势能是45J |
| D.动能与势能相等的时刻一定出现在撤去力F之前 |
如图(a)所示,用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图像如图(b)所示,若重力加速度g取10m/s2。根据图(b)中所提供的信息可以计算出
| A.物体的质量 | B.斜面的倾角 |
| C.斜面的长度 | D.加速度为6m/s2时物体的速度 |
某质点做匀变速直线运动的位移x与时间t的关系式为x=5t+t2(各物理量均采用国际单位制单位),则该质点( )
| A.第2s内的位移是14 m | B.前2s内的平均速度是8 m/s |
| C.任意相邻的1s内的位移差都是1 m | D.任意1s内的速度增量都是2 m/s |
下图是用打点计时器打出一系列点的纸带,纸带固定在一个做匀加速直线运动的小车后面,A、B、C、D、E为选好的记数点。两邻两计数点间有四个点未画出,电源频率为50赫兹,则相邻两记数点间的时间间隔为 s。由以上数据可从纸带上求出小车在运动中的加速度a=_____m/s2,打点计时器打下C点时小车的瞬时速度vc=_____.m/s

当物体做匀加速直线运动时,则 )
| A.在任何相等时间内的位移都相等; |
| B.在任意两个连续相等时间内的位移差都相等; |
| C.第1秒内、第2秒内和第3秒内的位移之比为1:3:5; |
| D.速度和时间不一定成正比 |
匀变速直线运动是:( )
| A.位移随时间均匀变化的直线运动 |
| B.速度的大小和方向恒定不变的直线运动 |
| C.加速度随时间均匀变化的直线运动 |
| D.加速度的大小和方向恒定不变的直线运动 |
短跑运动员完成100米赛跑的过程可简化为匀加速直线运动和匀速直线运动两个阶段.在一次比赛中,某运动员用11.00秒跑完全程.已知该运动员在匀加速直线运动阶段的第2秒内通过的距离为7.5米.试求:
(1)运动员在匀加速直线运动阶段的加速度;
(2)运动员在匀加速直线运动阶段通过的距离.
从同一高度处,先后释放两个重物,甲释放一段时间后,再释放乙,则以乙为参考系,甲的运动形式为( )
| A.自由落体运动 | B.匀加速直线运动a<g |
| C.匀加速直线运动a>g | D.匀速直线运动 |
一劲度系数k="800" N/m的轻质弹簧两端分别连接着质量均为12 kg的物体A、B,将它们竖直静止放在水平面上,如图所示。现将一竖直向上的变力F作用在A上,使A开始向上做匀加速运动,经0.40 s物体B刚要离开地面,取g ="10" m/s2,试求这0.40s内力F所做的功。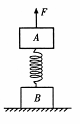
汽车以15m/s的速度做匀速直线运动,见前方有障碍物立即刹车,刹车的加速度大小为5m/s2,则汽车刹车后2s内及刹车后6s内通过的位移之比为多少?
甲、乙、丙三辆汽车以相同的速度同时经过某一路标,以后甲车一直做匀速直线运动,乙车先加速后减速,丙车先减速后加速,它们经过下一路标时的速度又相同,则下列说法中正确的是( )
| A.甲车先通过下一路标 | B.乙车先通过下一路标 |
| C.丙车先通过下一路标 | D.三车同时到达 |
如图甲、乙所示,为同一打点计时器打出的两条纸带,由纸带可知( )

| A.在打下计数点“0”至“5”的过程中,纸带甲的平均速度比乙的大 |
| B.在打下计数点“0”至“5”的过程中,纸带甲的平均速度比乙的小 |
| C.纸带甲的加速度比乙的大 |
| D.纸带甲的加速度比乙的小 |