如图所示，质量分别为mA＝1kg、mB＝3 kg的物块A、B置于足够长的水平面上，在F＝13 N的水平推力作用下，一起由静止开始向右做匀加速运动，已知A、B与水平面间的动摩擦因数分别为μA＝0.2、μB＝0.1，取g＝10 m/s2.求：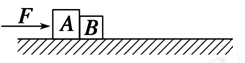
（1）物块A、B一起做匀加速运动的加速度；
（2）物块A对物块B的作用力大小；
（3）某时刻A、B的速度为v＝10 m/s，此时撤去推力F，求撤去推力后物块A、B间的最大距离．
如图所示，在粗糙水平面上有一质量为M=2kg的粗糙、绝缘斜面体，斜面的倾角
，在斜面体的左侧相距为d=1.5m处有一固定障碍物Q。将一质量为m=0.2kg，带电量为
的小物块（可视为质点）用绝缘绳系住，绳的一端固定在斜面体的顶端，此时小物块恰好能在斜面体上与斜面体一起保持静止且绳刚好伸直无弹力。现给斜面体施加一个水平向左的推力F，使斜面体和小物块一起向左做匀加速运动，当斜面体到达障碍物Q与其碰撞后，斜面体立即被障碍物Q锁定。已知斜面体与地面间的动摩擦因数为μ1=0.5，重力加速度g=10m/s2，设滑动摩擦力等于最大静摩擦力，求：
（1）小物块与绝缘斜面间的动摩擦因数μ2；
（2）最大的水平推力F；
（3）若用最大水平推力作用在斜面体上，斜面体被障碍物Q锁定后，小物块在绝缘绳牵引下沿圆周运动而不脱离圆轨道，轻绳的长度应满足的条件？
某电视台“快乐向前冲”节目的场地设施如图所示，AB为水平直轨道，上面安装有电动悬挂器，可以载人运动，水面上漂浮着一个半径为R、角速度为ω、铺有海绵垫的转盘，转盘的轴心离平台的水平距离为L，平台边缘与转盘平面的高度差为H。选手抓住悬挂器可以在电动机的带动下，从A点下方的平台边缘处沿水平方向做初速度为零、加速度为a的匀加速直线运动．选手必须作好判断，在合适的位置释放，才能顺利落在转盘上．设人的质量为m（不计身高），人与转盘间的最大静摩擦力为μmg，重力加速度为g.
（1）假设选手落到转盘上瞬间相对转盘速度立即变为零，为保证他落在任何位置都不会被甩下转盘，转盘的角速度ω应限制在什么范围？
（2）若已知H＝5 m，L＝8 m，a＝2 m/s2，g＝10 m/s2，且选手从某处C点释放能恰好落到转盘的圆心上，则他是从平台出发后多长时间释放悬挂器的？
（3）若电动悬挂器开动后，针对不同选手的动力与该选手重力关系皆为F=0.6mg，悬挂器在轨道上运动时存在恒定的摩擦阻力，选手在运动到上面（2）中所述位置C点时，因恐惧没有释放悬挂器，但立即关闭了它的电动机，则按照（2）中数据计算悬挂器载着选手还能继续向右滑行多远的距离？
如图所示，两个同心圆，半径分别为r和2r，在两圆之间的环形区域内存在垂直纸面向里的匀强磁场，磁感应强度为B。圆心O处有一放射源，放出粒子的质量为m，带电荷量为q，假设粒子速度方向都和纸面平行, 不计粒子重力。
（1）图中箭头表示某一粒子初速度的方向，OA与初速度方向夹角为60°，要想使该粒子经过磁场第一次通过A点，则初速度的大小是多少？
（2）要使粒子不穿出环形区域，则粒子的初速度不能超过多少？
如图所示，质量为0.3kg的小球A放在光滑的曲面上，离地面的高度0.2m，小球B静止在水平地面上，B离竖直墙的距离是
，A静止释放，与B发生弹性碰撞，B与墙碰撞无机械能损失，也不计B与墙碰撞时间，在离墙2.5m处两球发生第二次碰撞，重力加速度g=10m/s2，求：
①小球B的质量；
②两球第一次碰撞到第二次碰撞的时间间隔。
粤公网安备 44130202000953号