质量M＝0.2 kg的小圆环穿在固定的足够长的斜木杆上，斜木杆与水平方向的夹角θ＝37°，小圆环与木杆间的动摩擦因数μ＝0.5，小圆环受到竖直向上的恒定拉力F＝3 N后，由静止开始沿木杆斜向上做匀加速直线运动（sin37°＝0.6，cos37°＝0.8，g取10 m/s2），求：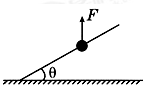
（1）小圆环沿斜木杆向上的合外力为多少；
（2）4 s末小圆环的速度为多少？
如图所示，倾角为θ＝30°的斜面固定在地面上，物体A与斜面间的动摩擦因数为μ＝
，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于B点，开始时物体A到B的距离为L＝1 m，现给A一个沿斜面向下的初速度v0＝2 m/s，使物体A开始沿斜面向下运动，物体A将弹簧压缩到最短后又恰好被弹回到B点，取g＝10 m/s2(不计空气阻力)，求：
(1)物体A第一次运动到B点时的速度大小．
(2)弹簧的最大压缩量．
如图所示，两根足够长、电阻不计、间距为d的光滑平行金属导轨，其所在平面与水平面的夹角为θ，导轨平面内的矩形区域abcd内存在有界匀强磁场，磁感应强度大小为B，方向垂直于导轨平面向上，ab与cd之间相距为L，金属杆甲、乙的阻值相同，质量均为m，甲杆在磁场区域的上边界ab处，乙杆在甲杆上方与甲相距L处，甲、乙两杆都与导轨垂直．静止释放两杆的同时，在甲杆上施加一个垂直于杆平行于导轨的外力F，使甲杆在有磁场的矩形区域内向下做匀加速直线运动，加速度大小为a＝2gsin θ，甲离开磁场时撤去F，乙杆进入磁场后恰好做匀速运动，然后离开磁场．
(1)求每根金属杆的电阻R.
(2)从释放金属杆开始计时，求外力F随时间t变化的关系式，并说明F的方向．
(3)若整个过程中，乙金属杆共产生热量Q，求外力F对甲金属杆做的功W.
如图所示，在xOy平面直角坐标系的第一象限有射线OA，OA与x轴正方向夹角为30°，OA与y轴所夹区域内有沿y轴负方向的匀强电场E1，第二象限存在水平向右的匀强电场E2，其它区域存在垂直于坐标平面向外的匀强磁场．有一质量为m、电荷量为q的带正电粒子，从y轴上的P点沿着x轴正方向以初速度v0射入电场，运动一段时间后经过Q点垂直于射线OA进入磁场，经磁场垂直x轴进入偏转电场E2，过y轴正半轴上的P点再次进入匀强电场E1，已知OP＝h，不计粒子重力，求：
(1)粒子经过Q点时的速度大小；
(2)匀强电场电场强度E1的大小；
(3)粒子从Q点运动到P点所用的时间．
如图所示，在第二象限和第四象限的正方形区域内分别存在着匀强磁场，磁感应强度均为B，方向相反，且都垂直于xOy平面．一电子由P(－d，d)点，沿x轴正方向射入磁场区域Ⅰ.(电子质量为m，电荷量为e，sin 53°＝
)
(1)求电子能从第三象限射出的入射速度的范围．
(2)若电子从
位置射出，求电子在磁场 Ⅰ 中运动的时间t.
(3)求第(2)问中电子离开磁场Ⅱ时的位置坐标．
如图所示的竖直平面内有范围足够大、水平向左的匀强电场，在虚线的左侧有垂直纸面向里的匀强磁场，磁感应强度大小为B，一绝缘轨道由两段直杆和一半径为R的半圆环组成，固定在纸面所在的竖直平面内，PQ、MN水平且足够长，半圆环MAP在磁场边界左侧，P、M点在磁场边界线上，NMAP段光滑，PQ段粗糙．现有一质量为m、带电荷量为＋q的小环套在MN杆上，它所受到的电场力为重力的1/2.现将小环从M点右侧的D点由静止释放，小环刚好能到达P点．
(1)求D、M间距离x0；
(2)求上述过程中小环第一次通过与O等高的A点时半圆环对小环作用力的大小；
(3)若小环与PQ间动摩擦因数为μ(设最大静摩擦力与滑动摩擦力大小相等)，现将小环移至M点右侧5R处由静止释放，求小环在整个运动过程中克服摩擦力所做的功．
粤公网安备 44130202000953号