研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间) ,但饮酒会导致反应时间延长,在某次试验中,志愿者少量饮酒后驾车以
,但饮酒会导致反应时间延长,在某次试验中,志愿者少量饮酒后驾车以 的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m。减速过程中汽车位移s与速度v的关系曲线如图乙所示,此过程可视为匀变速直线运动。取重力加速度的大小g=10m/s2。求:
的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m。减速过程中汽车位移s与速度v的关系曲线如图乙所示,此过程可视为匀变速直线运动。取重力加速度的大小g=10m/s2。求: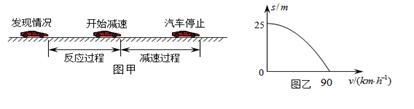
(1)减速过程汽车加速度的大小及所用时间;
(2)饮酒使志愿者的反应时间比一般人增加了多少?
(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值。
研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间) ,但饮酒会导致反应时间延长,在某次试验中,志愿者少量饮酒后驾车以
,但饮酒会导致反应时间延长,在某次试验中,志愿者少量饮酒后驾车以 的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m。减速过程中汽车位移s与速度v的关系曲线如图乙所示,此过程可视为匀变速直线运动。取重力加速度的大小g=10m/s2。求:
的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m。减速过程中汽车位移s与速度v的关系曲线如图乙所示,此过程可视为匀变速直线运动。取重力加速度的大小g=10m/s2。求:
(1)减速过程汽车加速度的大小及所用时间;
(2)饮酒使志愿者的反应时间比一般人增加了多少?
(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值。