在一次执行特殊任务的过程中，飞行员在距地面80m高的水平面上做匀加速直线运动的某波音轻型飞机上依次抛出a、b、c三个物体，抛出的时间间隔为1s，抛出点a、b与b、c间距分别为45m和55m，三个物体分别落在水平地面上的A、B、C三处．求：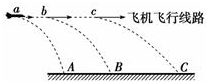
（1）飞机飞行的加速度；
（2）刚抛出b物体时飞机的速度大小；
（3）b、c两物体落地点B、C间的距离．
相关试题
如图所示，有一质子（电量为e，质量为m）由静止经电压U1加速后，进入两块间距为d电压为U2的平行金属板间，若质子从两板正中间垂直电场方向射入，且正好能从下板右边缘穿出电场，求
质子则进入偏转电场U2时的速度
在偏转电场U2中运动的时间和金属板的长L
质子穿出电场时的动能
如图所示，电源的电动势E=110V，电阻R1=21Ω，电动机线圈的电阻R0=0.5Ω，电键S1始终闭合。当电键S2断开时，电阻R1的电功率是525W；当电键S2闭合时，电阻R1的电功率是336W，求
电源的内电阻；
当电键S2闭合时流过电源的电流和电动机的输出功率。
公共汽车从车站由静止以1 m/s2的加速度匀加速开出,司机发现有乘客未上车,急忙刹车.车匀减速停下,整个过程历时5s,车前进了10m，求汽车在此过程中最大速度
匀加速运动的时间
匀减速运动的加速度
粤公网安备 44130202000953号