如图所示，质量为mB=14kg的木板B放在水平地面上，质量为mA=10kg的木箱A放在木板B上。一根轻绳一端拴在木箱上，另一端拴在地面的木桩上，绳绷紧时与水平面的夹角为θ=37°。已知木箱A与木板B之间的动摩擦因数μ1=0.5，木板B与地面之间的动摩擦因数μ2=0.4。重力加速度g取10m/s2。现用水平力F将木板B从木箱A下面匀速抽出，试求：（sin37°=0.6，cos37°=0.8）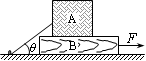
（1）绳上张力FT的大小；
（2）拉力F的大小。
如图甲所示，在磁感应强度为B的水平匀强磁场中，有两根竖直放置相距为L平行光滑的金属导轨，顶端用一阻直为R的电阻相连，两导轨所在的竖直平面与磁场方向垂直。一根质量为m的金属棒从静止开始沿导轨竖直向下运动，当金属棒下落龙时，速度达到最大，整个过程中金属棒与导轨保持垂直且接触良好。重力加速度为g，导轨与金属棒的电阻可忽略不计，设导轨足够长。求：
（l）通过电阻R的最大电流；
（2）从开始到速度最大过程中，金属棒克服安培力做的功WA；
（3）若用电容为C的平行板电容器代替电阻R，如图乙所示，仍将金属棒从静止释放，经历时间t的瞬时速度v1。
如图所示，在石轴上方存在匀强磁场，磁感应强度为B，方向垂直纸面向内。在x轴下方存在匀强电场，方向竖直向上。一个质量为m，电荷量为q，重力不计的带正电粒子从y轴上的a(h、0)点沿y正方向以某初速度开始运动，一段时间后，粒子与x轴正方向成45°进入电场，再次经过y轴的b点时速度方向恰好与y轴垂直。求：
（1）粒子在磁场中运动的轨道半径厂和速度大小v1；
（2）匀强电场的电场强度大小E；
（3）粒子从开始到第三欢经过x轴的时间t总
如图甲所示，质量m="l" kg的物块在平行斜面向上的拉力尸作用下从静止开始沿斜面向上运动，t=0.5s时撤去拉力，利用速度传感器得到其速度随时间的变化关系图象（v-t图象）如图乙所示，g取l0m／s2，求：
（1）2s内物块的位移大小s和通过的路程L；
（2）沿斜面向上运动两个阶段加速度大小a1、a2和拉力大小F。
如图所示，在足够长的绝缘板MN上方距离为d的O点处，水平向左发射一个速率为v0，质量为
、电荷为
的带正电的粒子（不考虑粒子重力）。
（1）若在绝缘板上方加一电场强度大小为
、方向竖直向下的匀强电场，求带电粒子打到板上距P点的水平距离（已知
）；
（2）若在绝缘板的上方只加一方向垂直纸面，磁感应强度
的匀强磁场，求：①带电粒子在磁场中运动半径； ②若O点为粒子发射源，能够在纸面内向各个方向发射带电粒子（不考虑粒子间的相互作用），求发射出的粒子打到板上的最短时间。
的正离子从静止开始经加速后，恰好通过速度选择器，从a孔以平行于ab方向进入abcd磁场区，正离子刚好经过小孔S 打在荧光屏上。求：
粤公网安备 44130202000953号