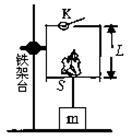
(10分)、“拔火罐”是一种中医疗法，为了探究“火罐”的“吸力”，某人设计了如下图实验。圆柱状气缸（横截面积为S）被固定在铁架台上，轻质活塞通过细线与重物m相连。将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内，酒精棉球熄灭时（设此时缸内温度为t°C）密闭开关K，此时活塞下的细线刚好拉直且拉力为零，而这时活塞距缸底为L.由于气缸传热良好，重物被吸起，最后重物稳定在距地面L/10处。已知环境温度为27°C不变，mg/s与1/6大气压强相当，气缸内的气体可看做理想气体，求t值。