如图所示,一质量为m=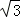 ×10﹣2kg,带电量为q=10﹣6C的小球(可视为质点),用绝缘细线悬挂在水平向右的匀强电场中的定点O,设电场足够大,静止时悬线向右与竖直方向成30°角.重力加速度g=10m/s2. 则:
×10﹣2kg,带电量为q=10﹣6C的小球(可视为质点),用绝缘细线悬挂在水平向右的匀强电场中的定点O,设电场足够大,静止时悬线向右与竖直方向成30°角.重力加速度g=10m/s2. 则:
(1)求电场强度E;
(2)若在某时刻将细线突然剪断,设定点O距离地面的竖直高度为H=10m,绳长L=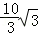 m,求小球的落地时间(小球在运动过程电量保持不变).
m,求小球的落地时间(小球在运动过程电量保持不变).
如图所示,一质量为m=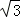 ×10﹣2kg,带电量为q=10﹣6C的小球(可视为质点),用绝缘细线悬挂在水平向右的匀强电场中的定点O,设电场足够大,静止时悬线向右与竖直方向成30°角.重力加速度g=10m/s2. 则:
×10﹣2kg,带电量为q=10﹣6C的小球(可视为质点),用绝缘细线悬挂在水平向右的匀强电场中的定点O,设电场足够大,静止时悬线向右与竖直方向成30°角.重力加速度g=10m/s2. 则:
(1)求电场强度E;
(2)若在某时刻将细线突然剪断,设定点O距离地面的竖直高度为H=10m,绳长L=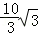 m,求小球的落地时间(小球在运动过程电量保持不变).
m,求小球的落地时间(小球在运动过程电量保持不变).