拖把是由拖杆和拖把头构成的擦地工具（如图）。设拖把头的质量为m，拖杆质量可以忽略；拖把头与地板之间的动摩擦因数为常数μ，重力加速度为g，某同学用该拖把在水平地板上拖地时，沿拖杆方向推拖把，拖杆与竖直方向的夹角为θ。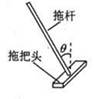
（1）若拖把头在地板上匀速移动，求推拖把的力的大小。
（2）设能使该拖把在地板上从静止刚好开始运动的水平推力与此时地板对拖把的正压力的比值为λ。已知存在一临界角θ0，若θ≤θ0，则不管沿拖杆方向的推力多大，都不可能使拖把从静止开始运动。求这一临界角的正切tanθ0。
相关试题
已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v1的表达式；
（2）若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h，求卫星的运行周期T.
如图所示，一光滑的半径为R的圆形轨道放在水平面上，一个质量为m的小球以某一速度冲上轨道，当小球将要从轨道口飞出时，小球对轨道的压力恰好为零，则小球落地点C距A处多远？落地时速度多大？
一质量为m=2kg的木块放在水平地面上，由静止开始运动，受水平拉力F情况如图所示，已知木块与地面之间的动摩擦因数μ=0.2,求前8s内力F（不包括摩擦力）对木块所做的功。（取g=10m/s2）
2008年9月，神舟七号载人航天飞行获得了圆满成功，我国航天员首次成功实施空间出舱活动、飞船首次成功实施释放小伴星的实验，实现了我国空间技术发展的重大跨越．已知飞船在地球上空的圆轨道上运行时离地面的高度为h．地球半径为R，地球表面的重力加速度为g．求飞船在该圆轨道上运行时：
（1）速度v的大小；
（2）速度v与地球第一宇宙速度的比值。
粤公网安备 44130202000953号