如图所示，在竖直平面坐标系xOy的第一象限与第二象限虚线右侧空间内有垂直平面向外的水平匀强磁场和竖直向上的匀强电场，其磁感应强度大小和电场强度大小分别为B和E，第四象限内有垂直于平面向里的水平匀强电场，电场强度大小也为E，第三象限内有一绝缘光滑竖直的半圆轨道，轨道半径为R，最高点与坐标原点O相切，最低点与绝缘光滑水平面相切于N，在第二象限虚线上某点P处有一质量为m的带电小球(重力不可忽略)，沿与竖直方向成30°角斜向右上方进入正交的电场和磁场区域恰好做匀速圆周运动，且恰好通过坐标原点O，并沿水平方向切入半圆轨道并恰好能始终沿半圆轨道内侧运动，过N点后沿水平方向进入第四象限的电场中，已知重力加速度为g。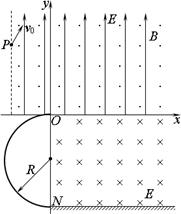
（1）判断小球的带电性质并求出带电荷量；
（2）求出入射点P的坐标；
（3）从小球通过N点开始计时，经时间t＝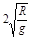
，小球距O点的距离s为多远？
如图所示，质量为m的滑块，在水平力作用下静止在倾角为θ在光滑斜面上，斜面的末端B与水平传送带相接，传送带的运行速度为v0，长为L；今将水平力撤去，当滑块滑到传送带右端C时，恰好与传送带速度相同。滑块与传送带间的动摩擦因数为μ。求：
（1）水平作用力力F大小；
（2）滑块下滑高度。
（3）若滑块进入传送带速度大于传送带的速度，滑块在传送带上滑行 的整个过程中产生的热量。
机动车驾驶执照考试的其中一个项目是定点停车：要求考生根据考官的指令在一路边标志杆旁停车。在一次练习中，车以一定速度匀速行驶，在距标志杆距离为s时，教练命令考生到标志杆停车，考生立即刹车，车在阻力f1作用下做匀减速直线运动，经一段时间，车刚好停在标志杆旁。第二次练习时，车以同样的初速度匀速行驶，教练在同样的位置命令考生到标志杆停车，考生迟了
时间才刹车，最后车也刚好停在标志杆旁。已知车和人总质量为M，车视为质点。求：
（1）车行驶的初速度是多少？
（2）第二次车做匀减速运动时受到的阻力f2是多少？
传送带以恒定速度v="1.2" m/s运行, 传送带与水平面的夹角为θ=37º。现将质量m="20" kg的物品轻放在其底端，经过一段时间物品被送到h=1.8m高的平台上，如图所示。已知物品与传送带之间的动摩擦因数μ=0.85，则：（sin370=0.6，cos370=0.8，g="10" m/s2）
（1）物品从传送带底端到平台上所用的时间是多少？
（2）物块上升到平台过程机械能增加了多少？
（3）每送一件物品电动机多消耗的电能是多少？
汽车发动机的额定功率为
KW，质量为
kg，当汽车在水平路面上行驶时受到阻力为车重的
倍，若汽车从静止开始保持1 m／s2的加速度作匀加速直线运动，则
（1）汽车在路面上能达到的最大速度；
（2）匀加速直线运动过程能持续多长时间；
（3）当汽车速度为10 m/s时的加速度。
粤公网安备 44130202000953号