如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD的光滑,内圆A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑。一质量m=0.1kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,球运动的半径R=0.2m,取g=10m/s2。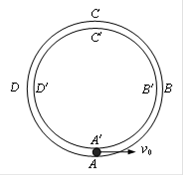
(1)若要使小球始终紧贴外圆做完整的圆周运动,初速度v0至少为多少?
(2)若v0=3m/s,经过一段时间小球到达最高点,内轨道对小球的支持力N=1N,则小球在这段时间内克服摩擦力做的功是多少?
(3)若v0=3m/s,经过足够长的时间后,小球经过最低点A时受到的支持力为多少?小球在整个运动过程中减少的机械能是多少?

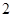 .求:
.求: ,Q点的坐标为
,Q点的坐标为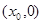 ,平行板电容器AB、CD两带电板平行于x轴,上板带正电,板长为
,平行板电容器AB、CD两带电板平行于x轴,上板带正电,板长为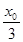 ,两板间的距离为
,两板间的距离为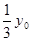 ,现有一质量为m,电量为+q的带电粒子从P点以初速度大小
,现有一质量为m,电量为+q的带电粒子从P点以初速度大小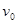 垂直于y轴射入第一象限,欲使这个粒子从Q点射出,且有最大的偏转角,需将电容器平移至第一象限的适当位置,不计粒子的重力,求
垂直于y轴射入第一象限,欲使这个粒子从Q点射出,且有最大的偏转角,需将电容器平移至第一象限的适当位置,不计粒子的重力,求
 ,已知重力加速度为g=10m/s2,求:
,已知重力加速度为g=10m/s2,求:
 粤公网安备 44130202000953号
粤公网安备 44130202000953号