某兴趣小组对一辆自制遥控小车的性能进行研究。他们让这辆小车在水平的直轨道上由静止开始运动，并将小车运动的全过程记录下来，通过处理转化为v—t图象，如图所示（除2s—10s时间段图象为曲线外，其余时间段图象均为直线）。已知在小车运动的过程中，2s—14s时间段内小车的功率保持不变，在14s末停止遥控而让小车自由滑行，小车的质量为1.0kg，可认为在整个运动过程中小车所受到的阻力大小不变。求：
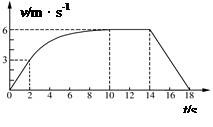
（1）小车所受到的阻力大小；
（2）小车匀速行驶阶段的功率；
（3）小车在加速运动过程中位移的大小。
相关试题
某物体做匀加速直线运动，加速度为2 m/s2，通过A点时速度为2m/s，通过B点时速度为6m/s，则：
（1）物体从A点运动到B点的时间为多长？
（2）A、B两点之间的距离是多少？
如图所示，将质量m=0.2kg的物体从高h=20m的山崖上A点斜向上抛出，抛出的速度大小V0=15m/s，以B点所在的平面为参考面，不计空气阻力，g取10m/s2．求
（1）物体在A点的动能Ek；
（2）物体在A点的重力势能Ep；
（3）物体落到B点的速度大小VB．
质量为50kg的物体放置在电梯内，电梯由静止开始向上运动，加速度为2m/s2，g=10m/s2．求：
（1）物体受到的支持力大小
（2）2s末物体的速度大小．
如图所示，跟水平面成θ=37°角且连接电源的光滑金属框架宽L=20cm，一根重为G的金属棒ab水平放在金属框架，磁感应强度B=0.6T，方向竖直向上，金属棒ab的电阻Rab=1Ω，电源电动势为25V，内阻r=1Ω，当滑动变阻器的电阻为3Ω时，金属棒刚好处于静止状态．
（1）求通过金属棒的电流大小
（2）求金属棒的重力大小？（sin 37°=0.6，cos37°=0.8）
粤公网安备 44130202000953号