如图所示,轻杆长1 m,其两端各连接质量为1 kg的小球,杆可绕距B端0.2 m的轴O在竖直平面内自由转动,轻 杆从静止由水平转至竖直方向,A球在最低点时的速度为4 m/s.(g取10 m/s2)
杆从静止由水平转至竖直方向,A球在最低点时的速度为4 m/s.(g取10 m/s2)
求:(1)A球此时对杆的作用力大小及方向;
(2)B球此时对杆的作用力大小及方向。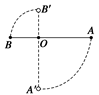
如图所示,轻杆长1 m,其两端各连接质量为1 kg的小球,杆可绕距B端0.2 m的轴O在竖直平面内自由转动,轻 杆从静止由水平转至竖直方向,A球在最低点时的速度为4 m/s.(g取10 m/s2)
杆从静止由水平转至竖直方向,A球在最低点时的速度为4 m/s.(g取10 m/s2)
求:(1)A球此时对杆的作用力大小及方向;
(2)B球此时对杆的作用力大小及方向。