理论研究表明,物体在地球附近都受到地球对它的万有引力作用,具有引力势能。选物体在距地球无限远处的引力势能为零,则引力势能可表示为Ep= —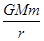 (其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离)。现有一质量m/的人造卫星绕地球做圆周运动周期T。若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)
(其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离)。现有一质量m/的人造卫星绕地球做圆周运动周期T。若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)
理论研究表明,物体在地球附近都受到地球对它的万有引力作用,具有引力势能。选物体在距地球无限远处的引力势能为零,则引力势能可表示为Ep= —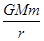 (其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离)。现有一质量m/的人造卫星绕地球做圆周运动周期T。若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)
(其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离)。现有一质量m/的人造卫星绕地球做圆周运动周期T。若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)