(11分) 如图所示，abcd是一个正方形盒子．cd边的中点有一个小孔e．盒子中有沿ad方向的匀强电场，一个质量为m带电粒子从a处的小孔沿ab方向以初速度v0射入盒内，并恰好从e处的小孔射出。求：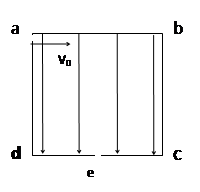
⑴该带电粒子从e孔射出时的速度大小。
⑵该过程中电场力对该带电粒子做的功。
B、C两个小球重量均为G，用细线悬挂在竖直墙上的A、D两点。细线与竖直墙壁之间的夹角分别为30o和60o （见图中标注），两个小球处于静止状态。求：
（1）AB和CD两根细线的拉力FAB和FCD 分别为多大？
（2）细线BC与竖直方向的夹角θ是多少？
如下图所示，A、B两物体叠放在水平地面上，已知A、B的质量分别为mA＝10 kg，mB＝20 kg，A、B之间，B与地面之间的动摩擦因数均为μ＝0.5.一轻绳一端系住物体A，另一端系于墙上，绳与竖直方向的夹角为37°，今欲用外力将物体B匀速向右拉出，求所加水平力F的大小．(取g＝10m/s2，sin 37°＝0.6，cos 37°＝0.8)
矿井里的升降机从静止开始做匀加速直线运动，经过3 s，它的速度达到3 m/s；然后做匀速运动，历时6 s；再做匀减速直线运动，经过3 s后停止。求升降机上升的高度，并画出它的速度时间图象。
运动场上4×800m接力赛已进入了白热化阶段，甲、乙两队都已经是最后一棒。甲队员健步如飞，最大速度达
=12m/s，乙队员也不甘落后奋力直追，可能是由于紧张，甲队员不小心将接力棒失落，回头拾起棒后，甲加速直追反超乙。现将甲的加速和减速过程都视为匀变速运动，且加速时的加速度大小
=2m/s2,减速时的加速度大小
=6m/s2，拾棒时的速度为零，不计棒脱手后的位移和拾棒动作所花的时间，问：（1）甲在返回拾棒过程中的最大速率为多少？
（2）甲因为拾棒而耽误了多少时间？
（3）若丢棒时甲领先乙△
=8m，而距离终点
=240m，乙的速度保持
=10m/s，通过计算分析甲能否赢得比赛？
粤公网安备 44130202000953号