如图所示,A、B两棒均长l m,A悬于高处,B竖于地面.A的下端和B的上端相距s="10" m.若A、B两棒同时运动,A做自由落体运动,B以初速度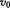 = 20m/s做竖直上抛运动,在运动过程中都保持竖直.问:
= 20m/s做竖直上抛运动,在运动过程中都保持竖直.问:
(1)两棒何时开始相遇?
(2)擦肩而过(不相碰)的时间?(取g="10" m/s2).
如图所示,A、B两棒均长l m,A悬于高处,B竖于地面.A的下端和B的上端相距s="10" m.若A、B两棒同时运动,A做自由落体运动,B以初速度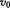 = 20m/s做竖直上抛运动,在运动过程中都保持竖直.问:
= 20m/s做竖直上抛运动,在运动过程中都保持竖直.问:
(1)两棒何时开始相遇?
(2)擦肩而过(不相碰)的时间?(取g="10" m/s2).