一种测定风作用力的仪器原理如图所示。它的细长丝线一端固定于O点,另一端悬挂着一个质量为m="1" kg的金属球。无风时,丝线自然下垂;当受到沿水平方向吹来的风的作用时,丝线将偏离竖直方向一定角度θ,风力越大,偏角越大。若某时刻丝线与竖直方向的夹角θ=37°,试求此时金属球所受风力的大小。(取g="10" m/s2,已知sin37°=0.6、cos37°=0.8)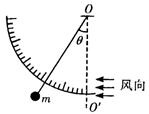
一种测定风作用力的仪器原理如图所示。它的细长丝线一端固定于O点,另一端悬挂着一个质量为m="1" kg的金属球。无风时,丝线自然下垂;当受到沿水平方向吹来的风的作用时,丝线将偏离竖直方向一定角度θ,风力越大,偏角越大。若某时刻丝线与竖直方向的夹角θ=37°,试求此时金属球所受风力的大小。(取g="10" m/s2,已知sin37°=0.6、cos37°=0.8)