如图所示,虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域,电场强度的
大小为E,方向向下,磁感应强度为B,方向垂直纸面向外,PQ为其分界线,现有一群质量为m,电荷
量为-e的电子(重力不计)从PQ中点与PQ成300。角以不同的初速射入磁场,求:(1)能从PQ边离开
磁场的电子在磁场运动的时间.
(2)若要电子在磁场运动时间最长,其初速v应满足的条件?
(3)若电子在满足(2)中的条件下且以最大速度进入磁场,最终从电场aP边界飞出虚线框所具有的动能Ek..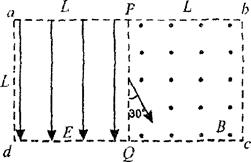
如图所示,虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域,电场强度的
大小为E,方向向下,磁感应强度为B,方向垂直纸面向外,PQ为其分界线,现有一群质量为m,电荷
量为-e的电子(重力不计)从PQ中点与PQ成300。角以不同的初速射入磁场,求:(1)能从PQ边离开
磁场的电子在磁场运动的时间.
(2)若要电子在磁场运动时间最长,其初速v应满足的条件?
(3)若电子在满足(2)中的条件下且以最大速度进入磁场,最终从电场aP边界飞出虚线框所具有的动能Ek..