甲、乙两运动员在训练交接棒的过程中发现：甲经短距离加速后能保持9 m/s的速度跑完全程；乙从起跑后到接棒前的运动是匀加速的．为了确定乙起跑的时机，需在接力区前适当的位置设置标记．在某次练习中，甲在接力区前x0＝13.5 m处作了标记， 并以v＝9 m/s的速度跑到此标记时向乙发出起跑口令．乙在接力区的前端听到口令时起跑，并恰好在速度达到与甲相同时被甲追上，完成交接棒．已知接力区的长度L＝20 m．求：
(1)此次练习中乙在接棒前的加速度a；
(2)在完成交接棒时乙离接力区末端的距离．
如图所示，穿过光滑水平平面中央小孔O的细线与平面上质量为m的小球P相连，手拉细线的另一端，让小球在水平面内以角速度ω1沿半径为a的圆周做匀速圆周运动。所有摩擦均不考虑。 求：
（1)这时细线上的张力多大？
(2)若突然松开手中的细线，经时间Δt再握紧细线，随后小球沿半径为b的圆周做匀速圆周运动。试问：Δt等于多大？这时的角速度ω2为多大？
如图所示．在水平面上固定一个半径为R的光滑球体，球的最高点处有一个小物体，现给小物体一个水平初速度，要使物体不沿球面下滑而做平抛运动，球落地点C到A点的最小距离.
在排球比赛中，运动员在离地3m处击中排球，使排球以15 m/s的速度水平飞出，若不计空气阻力，g取l0m/s2。 求
(1)排球落地点与击球点之间的水平距离；
(2) 离落地点为2m处的另—个运动员至少用多大的速度跑动，才能在球落地前接到球?
如图所示，足够长的光滑U形导体框架的宽度L =" 0.5" m，电阻忽略不计，其所在平面与水平面成
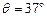角，磁感应强度B 
=" 0.8" T的匀强磁场方向垂直于导体框平面，一根质量m =" 0.2" kg，有效电阻R = 2Ω的导体棒MN垂直跨放在U形框架上，导体棒由静止开始沿框架下滑到刚开始匀速运动，通过导体棒截面的电量共为Q =" 2" C。求：
（1）导体棒匀速运动的速度；
（2）导体棒从开始下滑到刚开始匀速运动这一过程中，导体棒的电阻消耗的电功。（sin 37°=" 0.6 " cos 37°=" 0.8 " g = 10m/s2）
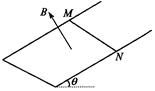
道放置在水平面上，两轨道间距L＝1m，电阻R＝1.0Ω；有一质量m=1kg的导体杆静止地放在轨道上，与两轨道垂直，杆及轨道的电阻可忽略不计，整个装置处于磁感强度B＝0.50T的匀强磁场中，磁场方向垂直轨道面向下．现用一外力F沿轨道方向拉杆，使之以a=
1m/s2的加速度做匀加速运动,速度达5m/s后导体杆做匀速直线运动,通过计算求出外力F与时间t的函数关系,并在下图中画出前10s内的F-t图象.
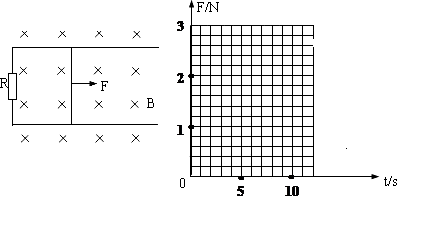
粤公网安备 44130202000953号