如图所示，一对平行光滑轨
道放置在水平面上，两轨道间距L＝1m，电阻R＝1.0Ω；有一质量m=1kg的导体杆静止地放在轨道上，与两轨道垂直，杆及轨道的电阻可忽略不计，整个装置处于磁感强度B＝0.50T的匀强磁场中，磁场方向垂直轨道面向下．现用一外力F沿轨道方向拉杆，使之以a=
1m/s2的加速度做匀加速运动,速度达5m/s后导体杆做匀速直线运动,通过计算求出外力F与时间t的函数关系,并在下图中画出前10s内的F-t图象.
相关试题
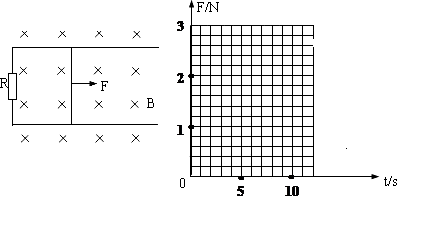
如图所示，一对平行光滑轨道放置在水平面上，两轨道间距L＝1m，电阻R＝1.0Ω；有一质量m=1kg的导体杆静止地放在轨道上，与两轨道垂直，杆及轨道的电阻可忽略不计，整个装置处于磁感强度B＝0.50T的匀强磁场中，磁场方向垂直轨道面向下．现用一外力F沿轨道方向拉杆，使之以a=1m/s2的加速度做匀加速运动,速度达5m/s后导体杆做匀速直线运动,通过计算求出外力F与时间t的函数关系,并在下图中画出前10s内的F-t图象.
,把
放在相距较远的两点，他们间作用力的大小为F，若使两球相接触后再分开放回原位置，求它们间作用力的大小．
C，
，让两绝缘金属小球接触，在接触的过程中，电子如何转移并转移了多少？
粤公网安备 44130202000953号