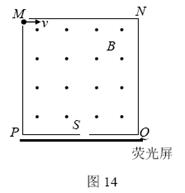
从粒子源不断发射相同的带电粒子,初速可忽略不计,这些粒子经电场加速后,从M孔以平行于MN方向进入一个边长为d的正方形的磁场区域MNQP,如图14所示,磁感应强度大小为B,方向垂直纸面向外,其中PQ的中点S开有小孔,外侧紧贴PQ放置一块荧光屏。当把加速电压调节为U时,这些粒子刚好经过孔S打在荧光屏上,不计粒子的重力和粒子间的相互作用。请说明粒子的电性并求出粒子的比荷(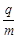 )
)
从粒子源不断发射相同的带电粒子,初速可忽略不计,这些粒子经电场加速后,从M孔以平行于MN方向进入一个边长为d的正方形的磁场区域MNQP,如图14所示,磁感应强度大小为B,方向垂直纸面向外,其中PQ的中点S开有小孔,外侧紧贴PQ放置一块荧光屏。当把加速电压调节为U时,这些粒子刚好经过孔S打在荧光屏上,不计粒子的重力和粒子间的相互作用。请说明粒子的电性并求出粒子的比荷(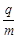 )
)