如图所示，空间存在着强度E=2.5×102N/C方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线，一端固定在O点，一端拴着质量m=0.5kg、电荷量q=4×10－2C的小球.现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.取g=10m/s2.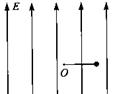
求：
（1）小球的电性；
（2）细线能承受的最大拉力；
（3）当小球继续运动后与O点水平方向距离为L时，小球距O点的高度.
如图所示，两根与水平面成θ＝30°角的足够长光滑金属导轨平行放置，导轨间距为L＝1m，导轨底端接有阻值为0.5W的电阻R，导轨的电阻忽略不计。整个装置处于匀强磁场中，磁场方向垂直于导轨平面斜向上，磁感应强度B＝1T。现有一质量为m＝0.2 kg、电阻为0.5W的金属棒用细绳通过光滑滑轮与质量为M＝0.5 kg的物体相连，细绳与导轨平面平行。将金属棒与M由静止释放，棒沿导轨运动了2 m后开始做匀速运动。运动过程中，棒与导轨始终保持垂直接触。（取重力加速度g=10m/s2）求：
（1）金属棒匀速运动时的速度；
（2）棒从释放到开始匀速运动的过程中，电阻R上产生的焦耳热；
（3）若保持某一大小的磁感应强度B1不变，取不同质量M的物块拉动金属棒，测出金属棒相应的做匀速运动的v值，得到实验图像如图所示，请根据图中的数据计算出此时的B1；
改变磁感应强度的大小为B2，B2＝2B1，其他条件不变，请在坐标图上画出相应的v—M图线，并请说明图线与M轴的交点的物理意义。
如图所示，长为l、内壁光滑的直管与水平地面成30°角固定放置，上端管口水平，且水平部分管口长度忽略不计，质量为m的小球可在直管内自由滑动，用一根轻质光滑细线将小球与另一质量为M的物块相连，M＝3m。开始时小球固定于管底，物块悬挂于管口，小球、物块均可视为质点。将小球释放，小球在管口的转向过程中速率不变。试求：
（1）物块落地前瞬间的速度大小；
（2）小球做平抛运动的水平位移；（M落地后绳子一直松弛）
（3）有同学认为，若取M＝km，则k足够大时，能使小球平抛运动水平位移的大小最大达到绳长l，请通过计算判断这种说法是否正确。
玻璃板生产线上，宽9 m的成型玻璃板以2 m/s的速度连续不断地向前行进，在切割工序处，金刚钻的走刀速度为10 m/s，为了使割下的玻璃板都成规定尺寸的矩形，金刚钻割刀的轨道应如何控制？切割一次的时间多长？
有一小船正在渡河，如图所示．在离对岸30 m时，其下游40 m处有一危险水域．假若水流速度为5 m/s，为了使小船在危险水域之前到达对岸，则小船从现在起相对于静水的最小速度应是多大？
粤公网安备 44130202000953号