有一个固定的光滑直杆，该直杆与水平面的夹角为53°，杆上套着一个质量为m=2kg的滑块（可视为质点）．
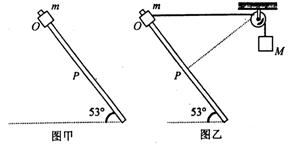
（1）如图甲所示，滑块从O点由静止释放，下滑了位移x=1m后到达P点，求滑块此时的速率．
（2）如果用不可伸长的细绳将滑块m与另一个质量为M=2.7kg的物块通过光滑的定滑轮相连接，细绳因悬挂M而绷紧，此时滑轮左侧绳恰好水平，其长度
m（如图乙所示）．再次将滑块从O点由静止释放，求滑块滑至P点的速度大小。
（整个运动过程中M不会触地，
）
在地面上有竖直放置的静止物体A和B，A、B之间用不计质量的轻弹簧栓接在一起，弹簧的劲度系数k=l00N/m，A、B的质量均为lkg，现用F=20N的竖直向上恒力作用在物体A上，使A竖直上升，重力加速度g=l0m/s2，设弹簧始终是在弹性限度内，空气阻力不计。求：（1）从力F开始作用到物体B刚离开地面的过程中拉力F做的功；
（2）物体B刚离开地面时物体A的速度大小；
一卡车拖挂一相同质量的车厢，在水平直道上以v0=12m/s的速度匀速行驶，其所受阻力可视为与车重成正比，与速度无关。某时刻，车厢脱落，并以大小为a=2m/s2的加速度减速滑行。在车厢脱落t=3s后，司机才发觉并紧急刹车，刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变，求卡车和车厢都停下后两者之间的距离。
在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后，到达最高点时高度为h，速度方向是水平的，速度大小为v0，求它第二次落到火星表面时速度的大小，计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r，周期为T。火星可视为半径为r0的均匀球体。
如图所示，半径为R，内径很小的光滑固定半圆管竖直放置，两个质量均为m的小球A、B，以不同的速度进入管内，A通过最高点C时，对管壁上部的压力为3mg，B通过最高点时，对管壁下部的压力为0.75mg。求A、B两球落地点间的距离。
绕OOˊ做匀速圆周运动时，弹簧长度为L2。求：
粤公网安备 44130202000953号