如图所示，开口向上竖直放置的内壁光滑气缸，其侧壁是绝热的，底部导热，内有两个质量均为m的密闭活塞，活塞A导热，活塞B绝热，将缸内理想气体分成Ⅰ、Ⅱ两部分。初状态整个装置静止不动处于平衡，Ⅰ、Ⅱ两部分气体的长度均为l₀，温度为T₀。设外界大气压强为P_o保持不变，活塞横截面积为S，且mg=P₀S，环境温度保持不变。求：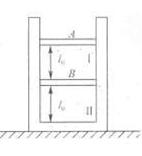

①在活塞A 上逐渐添加铁砂，当铁砂质量等于2m，两活塞在某位置重新处于平衡，活塞B下降的高度。
②现只对Ⅱ气体缓慢加热，使活塞A回到初始位置．此时Ⅱ气体的温度。