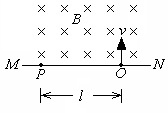图中MN表示真空室中垂直于纸面的平板，它的一侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度大小为B.一带电粒子从平板上的狭缝O处以垂直于平板的初速v射入磁场区域，最后到达平板上的P点.已知B、m、 v以及P到O的距离l，不计重力，求此粒子的电量q.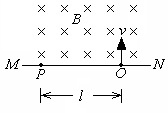
相关试题
汽车在平直的公路上以30m/s的速度匀速行驶，开始刹车后又以5m/s2的加速度做匀减速直线运动，求：
（1）从开始刹车后10秒钟汽车前进了多少米？
（2）静止前4s内汽车滑行的位移多大？
甲乙两辆汽车都从静止出发做加速直线运动，加速度方向一直不变．在第一段时间间隔内，两辆汽车的加速度大小不变，汽车乙的加速度大小是甲的两倍；在接下来的相同时间间隔内，汽车甲的加速度大小增加为原来的两倍，汽车乙的加速度大小减小为原来的一半．求甲乙两车各自在这两段时间间隔内走过的总路程之比．
粤公网安备 44130202000953号