如图甲所示为一列简谐横波某一时刻的波形图,已知该波沿+x方向连续传播,传播速度为2m/s。求
(1)波形图上x=2m处的质点P的振动周期,并在图乙给出的坐标轴上画出从该时刻计时的振动图象(画出一个周期的图象,在坐标轴上须标明标度)
(2)如图丙所示的装置中,在探究共振现象的实验中发现;当作用在装置上MN间驱动力的频率与上述横波的频率相同时,MN间五个单摆中的D摆恰好发生共振。现测得D摆摆线长L0=99.6cm。摆球的直径d=0.8cm,则当地重力加速度g为多少大?(结果取3位有效数字)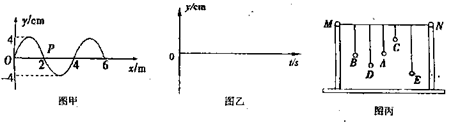
如图甲所示为一列简谐横波某一时刻的波形图,已知该波沿+x方向连续传播,传播速度为2m/s。求
(1)波形图上x=2m处的质点P的振动周期,并在图乙给出的坐标轴上画出从该时刻计时的振动图象(画出一个周期的图象,在坐标轴上须标明标度)
(2)如图丙所示的装置中,在探究共振现象的实验中发现;当作用在装置上MN间驱动力的频率与上述横波的频率相同时,MN间五个单摆中的D摆恰好发生共振。现测得D摆摆线长L0=99.6cm。摆球的直径d=0.8cm,则当地重力加速度g为多少大?(结果取3位有效数字)