质谱仪原理如图,a为粒子加速器电压为u1,b为速度选择器,磁场与电场正交,磁感强度为B1,板间距离为d,c为偏转分离器,磁感强度为B2,今有一质量为m,电量为+e的电子(不计重力),经加速后,该离子恰能通过速度选择器,粒子进入分离器后做匀速圆周运动,求:
(1)粒子的速率v
(2)速度选择器的电压u2
(3)粒子在B2的磁场中做匀速圆周运动的半径R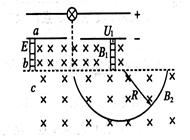
相关知识点
质谱仪原理如图,a为粒子加速器电压为u1,b为速度选择器,磁场与电场正交,磁感强度为B1,板间距离为d,c为偏转分离器,磁感强度为B2,今有一质量为m,电量为+e的电子(不计重力),经加速后,该离子恰能通过速度选择器,粒子进入分离器后做匀速圆周运动,求:
(1)粒子的速率v
(2)速度选择器的电压u2
(3)粒子在B2的磁场中做匀速圆周运动的半径R