截面积为0.2m2的100匝圆形线圈A处在匀强磁场中,磁场方向垂直线圈平面向里,如图所示,磁感应强度正按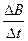 =0.02
=0.02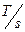 的规律均匀减小,开始时S未闭合。R1=4Ω,R2=6Ω,C=30µF,线圈内阻不计。求:
的规律均匀减小,开始时S未闭合。R1=4Ω,R2=6Ω,C=30µF,线圈内阻不计。求:
(1)S闭合后,通过R2的电流大小;
(2)S闭合后一段时间又断开,则S切断后通过R2的电量是多少?
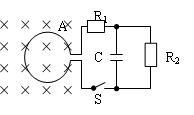
截面积为0.2m2的100匝圆形线圈A处在匀强磁场中,磁场方向垂直线圈平面向里,如图所示,磁感应强度正按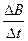 =0.02
=0.02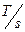 的规律均匀减小,开始时S未闭合。R1=4Ω,R2=6Ω,C=30µF,线圈内阻不计。求:
的规律均匀减小,开始时S未闭合。R1=4Ω,R2=6Ω,C=30µF,线圈内阻不计。求:
(1)S闭合后,通过R2的电流大小;
(2)S闭合后一段时间又断开,则S切断后通过R2的电量是多少?
