一细棒处于磁感应强度为B的匀强磁场中，棒与磁场垂直，与水平方向夹角为θ.磁感线水平指向纸内，如图11-42所示，棒上套一个可在其上滑动的带负电的小球C，小球质量为m，带电荷量为q，球与棒间动摩擦因数为μ，让小球从棒上端由静止下滑，求：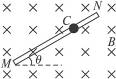
图11-42
(1) 小球的最大速度；
(2) 动摩擦因数μ应具备的条件.
相关试题
＝4.2×
N，起重杆的重为
＝2.0×
N。其他数据如图中所示。起重机至多能提起多重的货物？
将质量m=0.5kg的小球以初速度
=10m/s竖直上抛，经时间t=1.8s后小球落回原处，速度变为v=5m/s，在此过程中空气阻力f的大小始终不变，求：空气阻力f的大小。（g 取10m/
）
一个气球(包括所载之物)所受的重力为240N，以4m/s的速度匀速上升，升到距地面217m高处时，吊在气球下一质量为4kg的小石块因悬线断裂而脱离气球．求小石块刚着地时，气球距地面多高?(g取10m/
)
．
粤公网安备 44130202000953号