在LC振荡电路中，如已知电容C，并测得电路的固有振荡周期为T，即可求得电感L。为了提高测量精度，需多次改变C值并测得相应的T值。现将测得的六组数据标示在以C为横坐标，以T2为纵坐标的坐标纸上，即图中用“×”表示的点，如图14-2-7所示。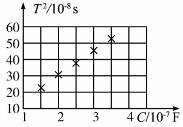
图14-2-7
(1)T、L、C的关系为_________________________________。
(2)根据图中给出的数据点做出T2与C的关系图线。
相关试题
如图所示，一个小球从光滑斜面上无初速地滚下，然后进入一个半径为0.5m的光滑圆形轨道的内侧，小球恰能通过轨道的最高点，求：
（1）小球离轨道最低点的高度。
（2）通过最低点时小球的向心加速度大小。（g＝10m/s2） 
长度为L的细线下挂一个质量为m的小球，小球半径忽略不计，现用一个水平力F拉小球使悬线偏离竖直方向θ角并保持静止状态，如图所示，撤掉F后，小球从静止开始运动到最低点时，求：
（1）小球的速度大小
（2）绳子拉力为多少？
将一个小球以
的速度沿水平方向抛出，小球经过
的时间落地。不计空气阻力作用。求：
（1）抛出点与落地点在竖直方向的高度差；
（2）小球落地时的速度大小
（3）以地面为零势能面，离地多高时动能是势能的3倍。
一列简谐横波在x轴上传播，在t1＝0和t2＝0.5 s两时刻的波形分别如图中的实线和虚线所示，求：
(1)周期
(2)波速
(3)若波速为92 m/s，求波的传播方向．
粤公网安备 44130202000953号