如图所示,一个圆筒形气缸平放在水平面上,A、B为两个可以无摩擦滑动的活塞,B活塞质量为m,A活塞的质量及厚度都可不计。B活塞用一根轻弹簧与气缸底相连,a、b为气缸侧壁上的两个小孔,与外界相通,两小孔及两活塞静止时的位置如左图所示。先用一根细管(细管容积不计)把a、b两孔连通,然后把气缸直立起来,并在A活塞上压一个质量也是m的砝码C,则B活塞下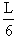 ,A活塞下降了
,A活塞下降了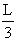 ,恰好挡住a孔,如右图所示。现在A活塞上再加一个与C相同的砝码D ,求A、B两活塞最后静止时的位置。(设温度始终保持不变)
,恰好挡住a孔,如右图所示。现在A活塞上再加一个与C相同的砝码D ,求A、B两活塞最后静止时的位置。(设温度始终保持不变) 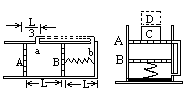
如图所示,一个圆筒形气缸平放在水平面上,A、B为两个可以无摩擦滑动的活塞,B活塞质量为m,A活塞的质量及厚度都可不计。B活塞用一根轻弹簧与气缸底相连,a、b为气缸侧壁上的两个小孔,与外界相通,两小孔及两活塞静止时的位置如左图所示。先用一根细管(细管容积不计)把a、b两孔连通,然后把气缸直立起来,并在A活塞上压一个质量也是m的砝码C,则B活塞下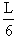 ,A活塞下降了
,A活塞下降了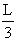 ,恰好挡住a孔,如右图所示。现在A活塞上再加一个与C相同的砝码D ,求A、B两活塞最后静止时的位置。(设温度始终保持不变)
,恰好挡住a孔,如右图所示。现在A活塞上再加一个与C相同的砝码D ,求A、B两活塞最后静止时的位置。(设温度始终保持不变) 