如图所示,两根相互平行,间距d=0.40m的金属导轨水平放置在磁感强度B=0.20T的匀强磁场中,磁场方向与轨道平面垂直,在导轨上,垂直导轨放置两根金属棒AB和CD,它们的总电阻R=0.20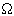 ,导轨电阻不计,当AB棒受到F=0.40N向左的水平拉力作用时,AB棒与CD棒分别以速度
,导轨电阻不计,当AB棒受到F=0.40N向左的水平拉力作用时,AB棒与CD棒分别以速度 作匀速运动,运动中AB和CD所受摩擦力相等.求两金属棒的速度差
作匀速运动,运动中AB和CD所受摩擦力相等.求两金属棒的速度差 等于多少?
等于多少?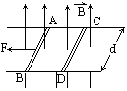
如图所示,两根相互平行,间距d=0.40m的金属导轨水平放置在磁感强度B=0.20T的匀强磁场中,磁场方向与轨道平面垂直,在导轨上,垂直导轨放置两根金属棒AB和CD,它们的总电阻R=0.20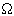 ,导轨电阻不计,当AB棒受到F=0.40N向左的水平拉力作用时,AB棒与CD棒分别以速度
,导轨电阻不计,当AB棒受到F=0.40N向左的水平拉力作用时,AB棒与CD棒分别以速度 作匀速运动,运动中AB和CD所受摩擦力相等.求两金属棒的速度差
作匀速运动,运动中AB和CD所受摩擦力相等.求两金属棒的速度差 等于多少?
等于多少?