在倾角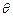
=30°的斜面上，固定一金属框，宽l=0.25m，接入电动势E=12V、内阻不计的电池．垂直框面放有一根质量m=0.2kg的金属棒ab，它与框架的动摩擦因数为
，整个装置放在磁感应强度B＝0.8T的垂直框面向上的匀强磁场中（如图11.2-５）．当调节滑动变阻器R的阻值在什么范围内时，可使金属棒静止在框架上？（设最大静摩擦力等于滑动摩擦力，框架与棒的电阻不计，g＝10m/s2）
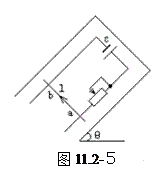
在倾角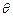=30°的斜面上，固定一金属框，宽l=0.25m，接入电动势E=12V、内阻不计的电池．垂直框面放有一根质量m=0.2kg的金属棒ab，它与框架的动摩擦因数为，整个装置放在磁感应强度B＝0.8T的垂直框面向上的匀强磁场中（如图11.2-５）．当调节滑动变阻器R的阻值在什么范围内时，可使金属棒静止在框架上？（设最大静摩擦力等于滑动摩擦力，框架与棒的电阻不计，g＝10m/s2）
粤公网安备 44130202000953号