光滑的长轨道形状如图所示,底部为半圆型,半径R,固定在竖直平面内。AB两质量相同的小环用长为R的轻杆连接在一起,套在轨道上。将AB两环从图示位置静止释放,A环离开底部2R。不考虑轻杆和轨道的接触,即忽略系统机械能的损失,求:
(1)AB两环都未进入半圆型底部前,杆上的作用力。
(2)A环到达最低点时,两球速度大小。
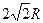 (3)若将杆换成长 ,A环仍从离开底部2R处静止释放,经过半圆型底部再次上升后离开底部的最大高度 。
(3)若将杆换成长 ,A环仍从离开底部2R处静止释放,经过半圆型底部再次上升后离开底部的最大高度 。 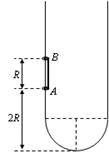
光滑的长轨道形状如图所示,底部为半圆型,半径R,固定在竖直平面内。AB两质量相同的小环用长为R的轻杆连接在一起,套在轨道上。将AB两环从图示位置静止释放,A环离开底部2R。不考虑轻杆和轨道的接触,即忽略系统机械能的损失,求:
(1)AB两环都未进入半圆型底部前,杆上的作用力。
(2)A环到达最低点时,两球速度大小。
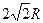 (3)若将杆换成长 ,A环仍从离开底部2R处静止释放,经过半圆型底部再次上升后离开底部的最大高度 。
(3)若将杆换成长 ,A环仍从离开底部2R处静止释放,经过半圆型底部再次上升后离开底部的最大高度 。 