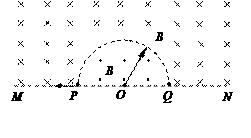
如图所示，直线MN下方无磁场，上方空间存在两个匀强磁场，其分界线是半径为R的半圆，两侧的磁场方向相反且垂直于纸面，磁感应强度大小都为B。现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出，最终打到Q点，不计微粒的重力。求：
（1）微粒在磁场中运动的周期；
（2）从P点到Q点，微粒的运动速度大小及运动时间；
（3）若向里磁场是有界的，分布在以O点为圆心、半径为R和2R的两半圆之间的区域，上述微粒仍从P点沿半径方向向左侧射出，且微粒仍能到达Q点，求其速度的最大值。