如图所示,质量为M的劈块,其左右劈面的倾角分别为θ1=30°θ2=45°,质量分别为m1=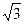 kg和m2=2.0kg的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ=0.20,求两物块下滑过程中(m1和m2均未达到底端)劈块受到地面的摩擦力。(g=10m/s2)
kg和m2=2.0kg的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ=0.20,求两物块下滑过程中(m1和m2均未达到底端)劈块受到地面的摩擦力。(g=10m/s2)
如图所示,质量为M的劈块,其左右劈面的倾角分别为θ1=30°θ2=45°,质量分别为m1=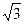 kg和m2=2.0kg的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ=0.20,求两物块下滑过程中(m1和m2均未达到底端)劈块受到地面的摩擦力。(g=10m/s2)
kg和m2=2.0kg的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ=0.20,求两物块下滑过程中(m1和m2均未达到底端)劈块受到地面的摩擦力。(g=10m/s2)