如图14-1所示,长为L,质量为m1的物块A置于光滑水平面上,在A的水平上表面左端放一质量为m2的物体B,B与A的动摩擦因数为μ。A和B一起以相同的速度V向右运动,在A与竖直墙壁碰撞过程中无机械能损失,要使B一直不从A上掉下来,V必须满足什么条件?(用m1、m2,L及μ表示)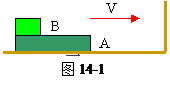
如图14-1所示,长为L,质量为m1的物块A置于光滑水平面上,在A的水平上表面左端放一质量为m2的物体B,B与A的动摩擦因数为μ。A和B一起以相同的速度V向右运动,在A与竖直墙壁碰撞过程中无机械能损失,要使B一直不从A上掉下来,V必须满足什么条件?(用m1、m2,L及μ表示)