湘教版必修三 7.1 解析几何初步练习卷
条件p:“直线l在y轴上的截距是在x轴上的截距的2倍”;条件q:“直线l的斜率为﹣2”,则p是q的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.非充分也非必要条件 |
已知直线l1的方向向量为a=(1,3),直线l2的方向向量b=(﹣1,k),若直线l2经过点(0,5),且l1⊥l2,则直线l2的方程为( )
| A.x+3y﹣5=0 | B.x+3y﹣15=0 | C.x﹣3y+5=0 | D.x﹣3y+15=0 |
与直线x+4y﹣4=0垂直,且与抛物线y=2x2相切的直线方程为( )
| A.4x﹣y+1=0 | B.4x﹣y﹣1=0 | C.4x﹣y﹣2=0 | D.4x﹣y+2=0 |
设点A(﹣2,3),B(3,2),若直线ax+y+2=0与线段AB没有交点,则a的取值范围是( )
A.(﹣∞,﹣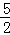 ]∪[ ]∪[ ,+∞) ,+∞) |
B.(﹣ , , ) ) |
C.[﹣ , , ] ] |
D.(﹣∞,﹣ ]∪[ ]∪[ ,+∞) ,+∞) |
△ABC的三个顶点为A(﹣3,0),B(2,1),C(﹣2,3),求:
(1)BC所在直线的方程;
(2)BC边上中线AD所在直线的方程;
(3)BC边上的垂直平分线DE的方程.
(1)求经过点A(﹣5,2)且在x轴上的截距等于在y轴上的截距的2倍的直线方程.
(2)过点A(8,6)引三条直线l1,l2,l3,它们的倾斜角之比为1:2:4,若直线l2的方程是y= x,求直线l1,l3的方程.
x,求直线l1,l3的方程.
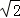
 ,
, ])的倾斜角的变化范围是( )
])的倾斜角的变化范围是( ) ,
, ]
] ,
, )
) ]
]

 的直线垂直,则实数a的值为 .
的直线垂直,则实数a的值为 . =(6,2),
=(6,2), =(﹣4,
=(﹣4, ),直线l过点A(3,﹣1),且与向量
),直线l过点A(3,﹣1),且与向量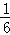 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号