江西省吉安市六校八年级下学期联考数学试卷
如图,将△ABC沿直线DE折叠后,使得点B与A重合。已知AC=5cm,△ADC的周长为17cm,则BC的长为( )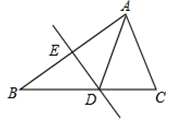
如图所示,直线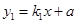 与
与 的交点坐标为(1,2)则使
的交点坐标为(1,2)则使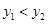 成立的x的取值范围为( )
成立的x的取值范围为( )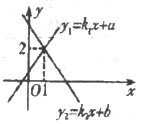
A.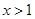 |
B.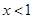 |
C.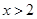 |
D.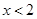 |
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下结论不成立的是( )
A.AD=BE B.AP=BQ C.DE=DP D.PQ∥AE
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D。若BD=10cm,BC=8cm,则点D到直线AB的距离是_____________cm。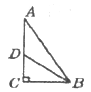
命题:直角三角形两条直角边的平方和等于斜边的平方,其逆命题是_____________。
如图,△ABC中

(1)画出△ABC关于x轴对称的△
(2)将△ABC绕原点O旋转180°,画出旋转后的△ 。
。
如图,△ABC的中线BD、CE交于点O,F、G分别是BO、CO的中点。
求证:四边形EFGD为平行四边形。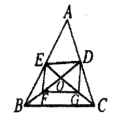
为了提高新产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场。现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍。
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
设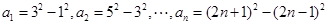 。(n为大于0的自然数)
。(n为大于0的自然数)
(1)探究an是否为8的倍数。
(2)若一个数的算术平方根是一个自然数,则称这个数是“完全平方数”,如:1,4,9就是完全平方数。试找出a1,a2,…,an,…,这一列数中从小到大排列的前4个完全平方数,并指出当n满足什么条件时,an为完全平方数。(不必说明理由)
如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P运动的时间为t(s),当t为何值时,△PBQ是直角三角形?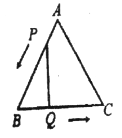
如图①,将两个完全相同的三角形纸片ABC与DEC重合放置,其中∠C=90°,∠B=∠E=30°。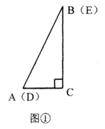
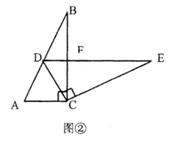
(1)如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,DE交BC于点F,则线段DF与AC有怎样的关系?请说明理由。
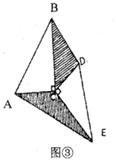
(2)当△DEC绕点C旋转到图③所示的位置时,设△BDC的面积为S1,△AEC的面积为S2。
猜想:S1与S2有怎样的数量关系?并证明你的猜想。
某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
| |
甲 |
乙 |
| 进价(元/部) |
4000 |
2500 |
| 售价(元/部) |
4300 |
3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元,[毛利润=(售价-进价)×销售量]
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过商场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量,已知乙种手机增加数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润。
 的解集是( )
的解集是( )



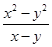 的结果是( )
的结果是( )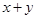
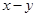
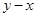
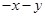
 是完全平方式,则m的值是( )
是完全平方式,则m的值是( )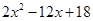 =_____________。
=_____________。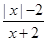 的值为零。
的值为零。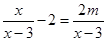 无解,则m=_____________。
无解,则m=_____________。
 的整数解。
的整数解。
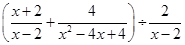 ,其中
,其中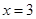
 粤公网安备 44130202000953号
粤公网安备 44130202000953号