高考名师推荐数学理科数列的概念、等差数列、等比数列
设Sn为等差数列{an}的前n项和,若a1=1,公差d=2,Sk+2-Sk=24,则k=" (" )
| A.8 |
| B.6 |
| C.5 |
| D.7 |
已知{an}是等差数列,a1=1,公差d≠0,Sn为其前 项和,若a1,a2,a5成等比数列,则S8="(" )
项和,若a1,a2,a5成等比数列,则S8="(" )
| A.50 |
| B.64 |
| C.62 |
| D.35 |
数列{an}的首项为3,{bn}为等差数列且bn=an+1-an (n∈N+).若b3=-2,b10=12,则a8="(" )
| A.0 |
| B.3 |
| C.8 |
| D.11 |
若等比数列{an}满足a2+a4=20,a3+a5=40,前100项和S100=( )
| A.2101 |
| B.2101+2 |
| C.2100-2 |
| D.2100 |
已知等比数列 的公比为q,记
的公比为q,记
 ,则以下结论一定正确的是( )
,则以下结论一定正确的是( )
A.数列 为等差数列,公差为 为等差数列,公差为 |
B.数列 为等比数列,公比为 为等比数列,公比为 |
C.数列 为等比数列,公比为 为等比数列,公比为 |
D.数列 为等比数列,公比为 为等比数列,公比为 |
已知首项为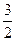 的等比数列{an}不是递减数列, 其前n项和为Sn(n∈N+), 且S3+ a3,S5+ a5,S4+ a4成等差数列,则数列{an}的通项公式为( )
的等比数列{an}不是递减数列, 其前n项和为Sn(n∈N+), 且S3+ a3,S5+ a5,S4+ a4成等差数列,则数列{an}的通项公式为( )
A.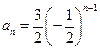 |
B.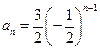 或 或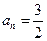 |
C.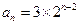 或 或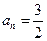 |
D.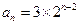 |
已知等比数列{an}是递增数列,Sn是{an}的前n项和.若a1,a3是方程x2-5x+4=0的两个根,则S6=( )
| A.63 |
| B.80 |
| C.73 |
| D.64 |
等差数列{an}的前n项和为Sn,已知S10=0,S15 =25,则nSn的最小值为 ( )
| A.-48 |
| B.-40 |
| C.-49 |
| D.-43 |
已知数列{an}满足3an+1+an=0,a2=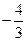 ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )
A.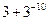 |
B.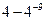 |
C.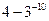 |
D.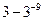 |
设等差数列{an}的前n项和为Sn,Sm-1=-2,Sm=0,Sm+1=3,则 = ( )
= ( )
| A.3 |
| B.4 |
| C.5 |
| D.6 |
等差数列{an}的前 项和为Sn.已知S3=
项和为Sn.已知S3= ,且S1,S2,S4成等比数列,则{an}的通项式为( )
,且S1,S2,S4成等比数列,则{an}的通项式为( )
| A.2n |
| B.2n-1 |
| C.2n+1或3 |
| D.2n-1或3 |
互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上OA和OB上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an若a1=1,a2=2则数列{an}的通项公式是_________.
古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10,…,第 个三角形数为
个三角形数为 =
= n2+
n2+ n。记第
n。记第 个
个 边形数为
边形数为
 ,以下列出了部分
,以下列出了部分 边形数中第
边形数中第 个数的表达式:
个数的表达式:
三角形数N(n,3)= n2+
n2+ n
n
正方形数N(n,4)=n2
五边形数N(n,5)= n2-
n2- n 六边形数N(n,6)=2n2-n
n 六边形数N(n,6)=2n2-n
……
可以推测 的表达式,由此计算
的表达式,由此计算 。
。
在正项等比数列{an}中,a5= ,a6+a7=3,则满足a1+a2+a3+…+an>a1a2a3…an的最大正整数
,a6+a7=3,则满足a1+a2+a3+…+an>a1a2a3…an的最大正整数 的值为 .
的值为 .
已知等差数列{an}满足a2=0,a6+a8=-10
(1)求数列{an}的通项公式;
(2)求数列{ }的前n项和.
}的前n项和.
设数列 的前
的前 项和为
项和为 .已知
.已知 ,
, =an+1-
=an+1- n2-n-
n2-n- (
( )
)
(1) 求 的值;
的值;
(2) 求数列 的通项公式;
的通项公式;
(3) 证明:对一切正整数 ,有
,有 +
+ +…+
+…+ <
< .
.
 sin
sin ,
, ,在
,在 中,正数的个数是( )
中,正数的个数是( ) 为等比数列,
为等比数列,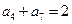 ,
,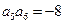 ,则
,则 ( )
( )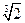 等比数列
等比数列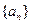 的各项都是正数,且
的各项都是正数,且 ,则
,则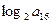 =( )
=( )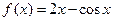 ,
,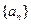 是公差为
是公差为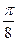 的等差数列,
的等差数列,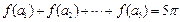 ,则
,则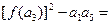 ( )
( )
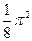
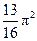
 ,则{an}的前
,则{an}的前 项和为
项和为  是首项为
是首项为 ,公差为
,公差为 的等差数列(d≠0),
的等差数列(d≠0), 是其前
是其前 项和.记bn=
项和.记bn= ,
, ,其中
,其中 为实数.
为实数. ,且
,且 ,
, ,
, 成等比数列,证明:Snk=n2Sk(k,n∈N+);
成等比数列,证明:Snk=n2Sk(k,n∈N+); 是等差数列,证明:
是等差数列,证明: 粤公网安备 44130202000953号
粤公网安备 44130202000953号