2014年高考数学（理）二轮专题复习真题感悟1-7练习卷

 ⁵展开式中的常数项为(　　)．

满足a，b∈{－1,0,1,2}，且关于x的方程ax²＋2x＋b＝0有实数解的有序数对(a，b)的个数为(　　)．

二项式(x＋y)⁵的展开式中，含x²y³的项的系数是________．(用数字作答)

将序号分别为1,2,3,4,5的5张参观券全部分给4人，每人至少1张，如果分给同一人的2张参观券连号，那么不同的分法种数是________．

从1,2,3,4中任取2个不同的数，则取出的2个数之差的绝对值为2的概率是(　　)．

A．	B．
C．	D．

如图，在矩形区域ABCD的A，C两点处各有一个通信 基站，假设其信号的覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源，基站工作正常)．若在该矩形区域内随机地选一地点，则该地点无信号的概率是(　　)．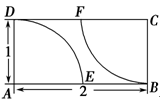

A．1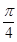－	B．－1
C．2－	D．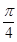

已知离散型随机变量X的分布列为

X	1	2	3
P

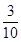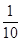则X的数学期望E(X)＝(　　)．
A.  B．2
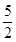C.  D．3

假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,50²)的随机变量，记一天中从甲地去乙地的旅客人数不超过900的概率为p₀.则p₀的值为(　　)．
(参考数据：若X～N(μ，σ²)，有P(μ－σ<X≤μ＋σ)＝0.682 6，P(μ－2σ<X≤μ＋2σ)＝0.954 4，P(μ－3σ<X≤μ＋3σ)＝0.997 4.

某学校有男、女学生各500名，为了解男、女学生在学习兴趣与业余爱好方面是否存在显著差异，拟从全体学生中抽取100名学生进行调查，则宜采用的抽样方法是(　　)．

某班的全体学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为：[20,40)，[40,60)，[60,80)，[80,100]．若低于60分的人数是15，则该班的学生人数是(　　)．

四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程，分别得到以下四个结论：
①y与x负相关且＝2.347x－6.423；
②y与x负相关且＝－3.476x＋5.648；
③y与x正相关且＝5.437x＋8.493；
④y与x正相关且＝－4.326x－4.578.
其中一定不正确的结论的序号是(　　)．

为了判断高中三年级学生是否选修文科与性别的关系，现随机抽取50名学生，得到如下2×2列联表：

已知P(K²≥3.841)≈0.05，P(K²≥5.024)≈0.025.
根据表中数据，得到k＝≈4.844.
则认为选修文科与性别有关系出错的可能性为________．