[广东]2014届广东省广州市萝岗区九年级上学期期末考试数学试卷
已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系是( )
| A.相交 | B.外切 | C.外离 | D.内含 |
书包里有数学书3本,英语书2本,语文书5本,从中任意抽取一本,是数学书的概率是( )
A. |
B. |
C. |
D. |
如图,△ABC是○O的内接三角形,若∠ABC=70°,则∠AOC的度数等于( )
| A.110° | B.130° | C.120° | D.140° |
某社区2012年投入教育经费2500万元,计划2014年投入3600万元,设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )
A.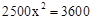 |
B.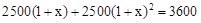 |
C. |
D. |
若圆锥的底面圆的周长是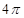 cm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数是( )
cm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数是( )
| A.40° | B.80° | C.120° | D.150° |
下列图形中,绕着它的中心点旋转60°后,可以和原图形重合的是( )
| A.正三角形 | B.正方形 | C.正五边形 | D.正六边形 |
如图,△ABC是⊙O的内接三角形,O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC= 
如图,二次函数 的图象经过x轴上的二点,它们的坐标分别是:(-4,0),(2,0).当x的取值范围是 时,y随x的增大而减小.
的图象经过x轴上的二点,它们的坐标分别是:(-4,0),(2,0).当x的取值范围是 时,y随x的增大而减小.
如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
在一个不透明的袋子中,装有3个除颜色外完全相同的小球,其中白球1个,黄球1个,红球1个,摸出一个球记下颜色后放回,再摸出一个球,请用列表法或画树状图法求:
(1)两次都摸出红球的概率;
(2)两次都摸到不同颜色球的概率.
如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙,墙长25m,另外三边用木栏围着,木栏长40m.
(1)若养鸡场面积为200 ,求鸡场靠墙的一边长;
,求鸡场靠墙的一边长;
(2)养鸡场面积能达到250 吗?如果能,请给出设计方案,如果不能,请说明理由.
吗?如果能,请给出设计方案,如果不能,请说明理由.
如图,已知:AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°.
(1)求证:CA=CD;
(2)求证:BD=OB.
已知抛物线 (m是常数,
(m是常数, )与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
(1)此抛物线的解析式;
(2)求点A、B、C的坐标.
如图,△ABC的两条高AD、CE相交于点H,D、E分别是垂足,过点C作BC的垂线交△ABC的外接圆于点F,求证:AH=FC.
 的值等于( )
的值等于( )

 的根是( )
的根是( )



 的最小值是( )
的最小值是( )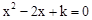 有两个不相等的实数根,则k的取值范围是( )
有两个不相等的实数根,则k的取值范围是( )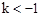



 有意义的x的取值范围是
有意义的x的取值范围是  的图象经过点(3,6),则
的图象经过点(3,6),则
 的一个根是-2,则另一个根是
的一个根是-2,则另一个根是  (2)解方程:
(2)解方程:
 、b在数轴上的位置如图所示,化简:
、b在数轴上的位置如图所示,化简:


 粤公网安备 44130202000953号
粤公网安备 44130202000953号