[云南]2014届云南省部分名校高三12月联考文科数学试卷
设全集U=R,集合A={x|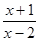
 },B={x|1<
},B={x|1< <8},则(CUA)∩B等于( )
<8},则(CUA)∩B等于( )
A.[-1,3) B.(0,2] C.(1,2] D.(2,3)
一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒,当某人到达路口时看见的是红灯的概率是( )
A. |
B.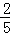 |
C. |
D.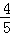 |
若函数f(x)=(k-1)ax-a-x(a>0,且a≠1)在R上既是奇函数,又是减函数,则g(x)=loga(x+k)的图象是( )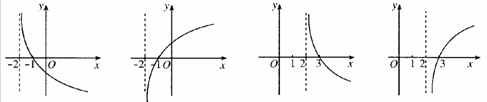
A. B. C. D.
函数y=sin(ωx+φ)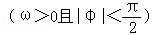 在区间
在区间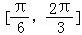 上单调递减,且函数值从1减小到﹣1,那么此函数图象与y轴交点的纵坐标为( )
上单调递减,且函数值从1减小到﹣1,那么此函数图象与y轴交点的纵坐标为( )
A. |
B. |
C.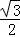 |
D.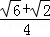 |
P是双曲线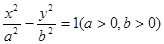 上的点,F1、F2是其焦点,且
上的点,F1、F2是其焦点,且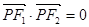 ,若△F1PF2的面积是9,a+b=7,则双曲线的离心率为( )
,若△F1PF2的面积是9,a+b=7,则双曲线的离心率为( )
A.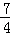 |
B. |
C.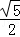 |
D.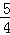 |
设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,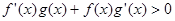 ,且
,且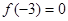 ,则不等式
,则不等式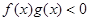 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列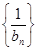 的前n项和.
的前n项和.
为预防H7N9病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
| 分组 |
A组 |
B组 |
C组 |
| 疫苗有效 |
673 |
a |
b |
| 疫苗无效 |
77 |
90 |
c |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(I)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取样本多少个?
(II)已知b≥465,c ≥30,求通过测试的概率
如图,已知在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.
(1)求证:平面EFG⊥平面PAD;
(2)若M是线段CD上一点,求三棱锥M﹣EFG的体积.
已知两点 及
及 ,点
,点 在以
在以 、
、 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)如图,动直线 与椭圆
与椭圆 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线
是直线 上的两点,且
上的两点,且 ,
, . 求四边形
. 求四边形 面积
面积 的最大值.
的最大值.
已知函数f(x)= ,x∈[1,3],
,x∈[1,3],
(1)求f(x)的最大值与最小值;
(2)若 于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.
于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.
已知曲线C的极坐标方程为 ,直线
,直线 的参数方程为
的参数方程为 ( t为参数,0≤
( t为参数,0≤ <
< ).
).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线 经过点(1,0),求直线
经过点(1,0),求直线 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
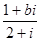 的实部与虚部相等,则实数b等于( )
的实部与虚部相等,则实数b等于( )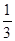

 满足
满足 则有( )
则有( )



 =(sinα,
=(sinα, )的模为
)的模为 ,则cos2α=( )
,则cos2α=( )

 ,则
,则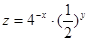 的最小值为( )
的最小值为( )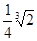
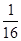
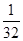
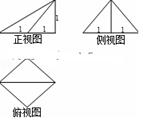
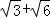
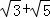
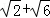
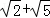
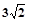 ,则正四棱锥的外接球的表面积为( )
,则正四棱锥的外接球的表面积为( )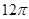

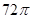
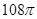
 ,则输入值
,则输入值 。
。
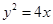 上任意一点,P在
上任意一点,P在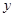 轴上的射影为Q,点M(4,5),则PQ与PM长度之和的最小值为 .
轴上的射影为Q,点M(4,5),则PQ与PM长度之和的最小值为 .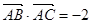 ,则
,则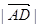 的最小值是______.
的最小值是______.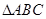 中,BC=
中,BC=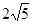 ,AC=2,
,AC=2, 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号